1. Probabilidade e aleatoriedade
Chamamos de probabilidade a percentagem de vezes que um certo evento aleatório aconteceria caso ele fosse repetido ou observado em um grande número de ocasiões subsequente.
A probabilidade de que uma moeda caia com o lado coroa é de 50% (ou 0,5), pois ao se observar um grande número de sequências de lançamento de moeda, essa seria a proporção de vezes em que coroa cairia para cima.
Podemos prever, com alto grau de certeza, que uma moeda arremessada 1.000.000 de vezes cairá cerca de 50% de vezes em cara e 50% das vezes em coroa. Porém, não podemos prever qual será o resultado da próxima jogada. Essa imprevisibilidade faz com que possamos qualificar o evento "queda da moeda com face coroa voltada para cima" como aleatório (random).
Quando lidamos com conjuntos de eventos aleatórios que têm um número reduzido de elementos (jogar a moeda 10 vezes, por exemplo), os resultados podem ser muito diferentes entre si. É muito possível que você tenha uma proporção de 60% ou 70% de coroas, em um conjunto de 10 lances.
Intuitivamente, sabemos que inferir uma regra geral de proporcionalidade a partir de 10 jogadas não deve funcionar bem. Mas, e se aumentarmos esse número para 100 jogadas? Já será suficiente para avaliarmos com segurança a proporcionalidade envolvida em lançar moedas?
E no caso de ações judiciais? Qual é a quantidade de processos que eu preciso analisar para poder extrapolar, com segurança, os dados do conjunto analisado para os dados da população de processos sobre a qual eu gostaria de fazer afirmações?
Quantas ADIs você precisa analisar para poder fazer afirmações seguras sobre tempo de tramitação, sobre tipos de argumentos utilizados, sobre o tipo de legislação impugnada? A leitura desse texto ajudará você a responder a essa questão, usando algumas abordagens estatísticas simples. Existem abordagens mais complexas, que darão respostas mais precisas, mas eles ultrapassam o escopo desta nossa abordagem introdutória.
Para responder a essas questões, é preciso ter em mente que nunca podemos saber, de antemão, o resultado de um evento aleatório. O fato de haver 50% de chance de sair coroa não nos diz nada sobre uma jogada específica. E o fato de ter saído coroa no primeiro lance não interfere em nada nas chances de sair coroa no segundo lance.
Isso é diferente do jogo de pedra-papel-tesoura, porque não é aleatória a escolha dos jogadores de usar uma dessas opções. Nesse jogo, é comum que a primeira rodada seja imprevisível, mas é muito comum que, em sua segunda rodada, os jogadores façam a escolha que seria vencedora caso o outro jogador repetisse a primeira jogada. E também é comum que, sabendo disso, alguns jogadores adaptem suas jogadas a essas expectativas.
Tampouco são aleatórias as decisões judiciais. Não é aleatório que uma ADI movida por uma parte ilegítima tenha sua inicial indeferida. Tampouco parece aleatória uma decisão pela qual um ministro concede uma liminar em uma ação movida por parte manifestamente ilegítima.
Nos dois parágrafos anteriores, usamos a noção comum de aleatoriedade, no sentido de eventos que não seguem padrões determinados. Porém, em termos estatísticos, esses eventos são, sim, aleatórios, na medida em que os resultados de um caso específico são imprevisíveis. Um evento é aleatório quando, se o repetirmos várias vezes, de forma semelhante, os resultados produzidos não podem ser previstos com certeza.
Certos resultados podem ser muito prováveis (como o indeferimento da inicial de partes consideradas ilegítimas pela jurisprudência do tribunal), mas eles não são necessários. Os cálculos probabilísticos não dizem nada sobre casos totalmente previsíveis, que chamamos de eventos determinísticos, nos quais não faz sentido avaliar os graus de probabilidade.
Quando você pode avaliar um evento como provável/improvável, ele é aleatório, e não determinístico.
Dada uma certa pressão atmosférica, não há dúvidas de que a água se congelará a certa temperatura. Uma moeda viciada, por exemplo, pode cair sempre para o mesmo lado, o que faz com que o seu arremesso não gere um evento aleatório. Um programa de computador típico oferece respostas idênticas ao mesmo input. E se o computador começar a responder de forma irregular aos mesmos estímulos, nossa suposição primária é a de que existe algo de errado com o software (um vírus, por exemplo) ou com o hardware (um superaquecimento que pode alterar o funcionamento previsto, por exemplo).
No caso de eventos determinísticos, a repetição de eventos similares não vai gerar resultados díspares, mas a constante repetição dos mesmos comportamentos. Esse tipo de infindável repetição não é esperada em vários tipos de fenômenos, como os biológicos: a própria manutenção da vida tem ocorrido pelo fato de que a reprodução celular envolver aleatoriedade. Os processos de replicação de DNA (ou RNA) propiciaram a manutenção de uma grande biodiversidade justamente porque se trada de um processo capaz de manter uma identidade quase completa com o modelo original, mas na qual sempre ocorrem algumas diferenças que são discretas e imprevisíveis.
Eventos aleatórios pode ser muito prováveis (como um ministro seguir a jurisprudência do tribunal ou a replicação exata de um gene no processo de reprodução celular), ou pouco prováveis (como uma ruptura jurisprudencial ou a mutação de um gene específico), mas eles não são totalmente previsíveis. No caso de ações judiciais, sempre é possível um resultado diverso, uma ruptura de padrões anteriores, uma invocação de circunstâncias especiais.
O interessante dos eventos aleatórios é que, embora não possamos prever o resultado de uma determinada ocorrência, podemos prever os graus de probabilidade de certas coisas ocorrerem. A estatística se relaciona justamente com a mensuração desses graus diversos de probabilidade.
Um evento aleatório típico é o lance de uma moeda. Além de aleatório, esse evento tem a peculiaridade de que seus dois resultados possíveis (cara e coroa) são igualmente prováveis. Mesmo que essa probabilidade seja idêntica, é possível que a moeda caia dez vezes seguidas em cara ou dez vezes seguidas em coroa. De fato, não é impossível que a sua moeda caia coroa um milhão de vezes seguidas, mas esse seria um resultado altamente improvável. O mais provável é que, quando observamos milhares de jogadas, os números de caras e coroas se equilibram ao longo do tempo.
Um número pequeno de ocorrências (por exemplo, algumas dezenas) pode nos dizer algo sobre fenômenos determinísticos (que ocorrem sempre do mesmo jeito), mas não nos dá segurança para fazer inferência acerca da probabilidade de eventos aleatórios. Toda avaliação segura da probabilidade depende da observação de um grande número de repetições. Essa é a chamada lei dos grandes números.
Quando analisamos um número restrito de casos (uma dezena de decisões, por exemplo), não podemos ter segurança de que a distribuição observada nesse conjunto segue o mesmo padrão da distribuição em um número grande de casos. Porém, a análise de um número grande de eventos (milhares de decisões, por exemplo) permite que tenhamos segurança em prever que os padrões de distribuição dos resultados sejam mantidos em números ainda maiores.
2. Curvas de distribuição
Curvas de distribuição, ou curvas de densidade, são representações gráficas da distribuição de um conjunto de dados em um contínuo, com referência a uma determinada medida. O gráfico abaixo, por exemplo, mostra a distribuição dos números de andamentos que têm as ADIs e as ADPFs ajuizadas de 1988 até 2020.
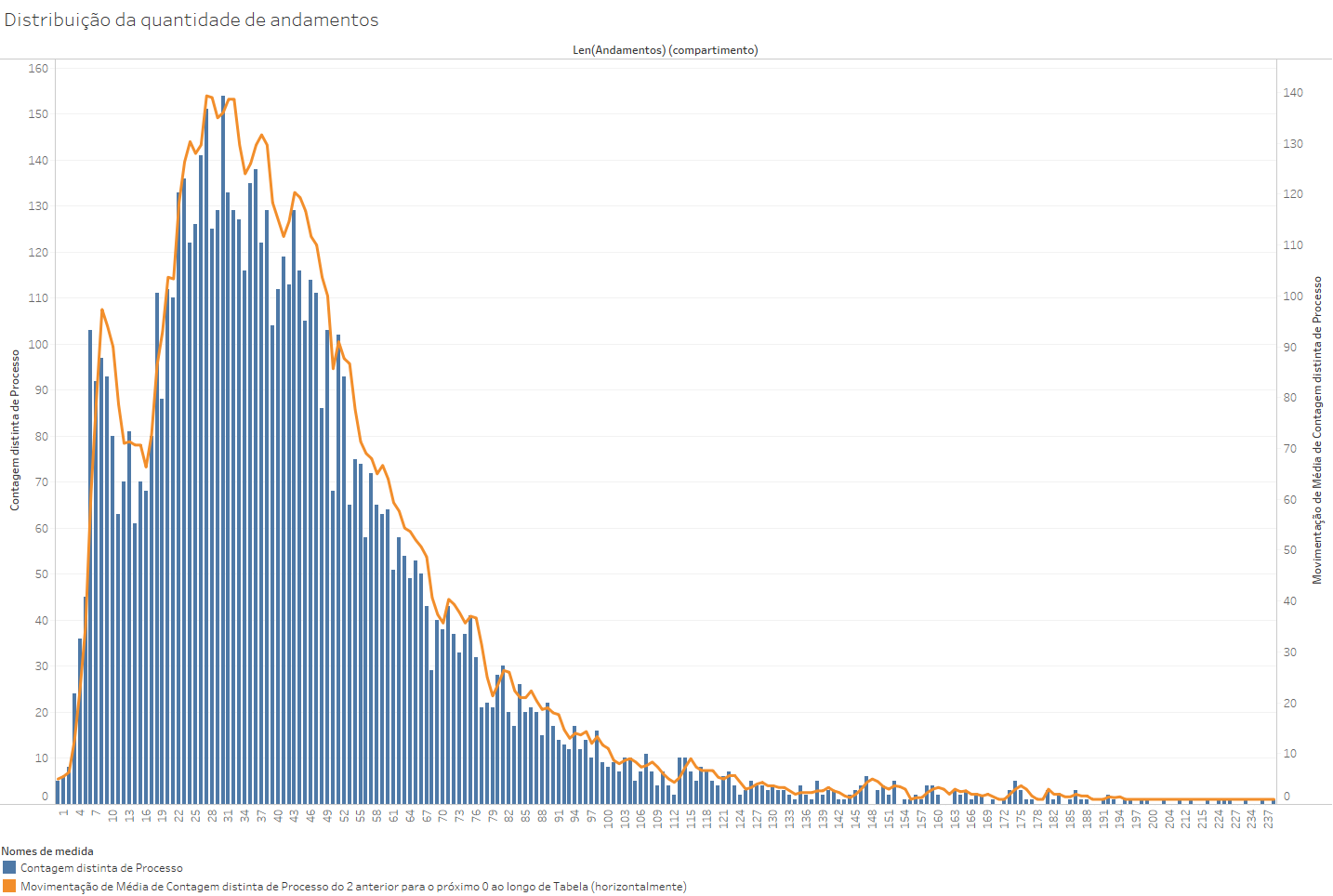
No Tableau, podemos construir gráficos de distribuição a partir de uma determinada medida. No caso acima a medida número de andamentos, contida na base ADIsADPFs(Andamentos). O tutorial para fazer gráficos desse tipo está no texto Como fazer um gráfico de Distribuição no Tableau.
Usando uma distribuição mais agregada e com menos ruído (com intervalos de 5 andamentos, em vez de 1 e com uma média móvel que envolve os 3 valores anteriores e os 3 valores posteriores), as mesmas informações geram o seguinte gráfico.
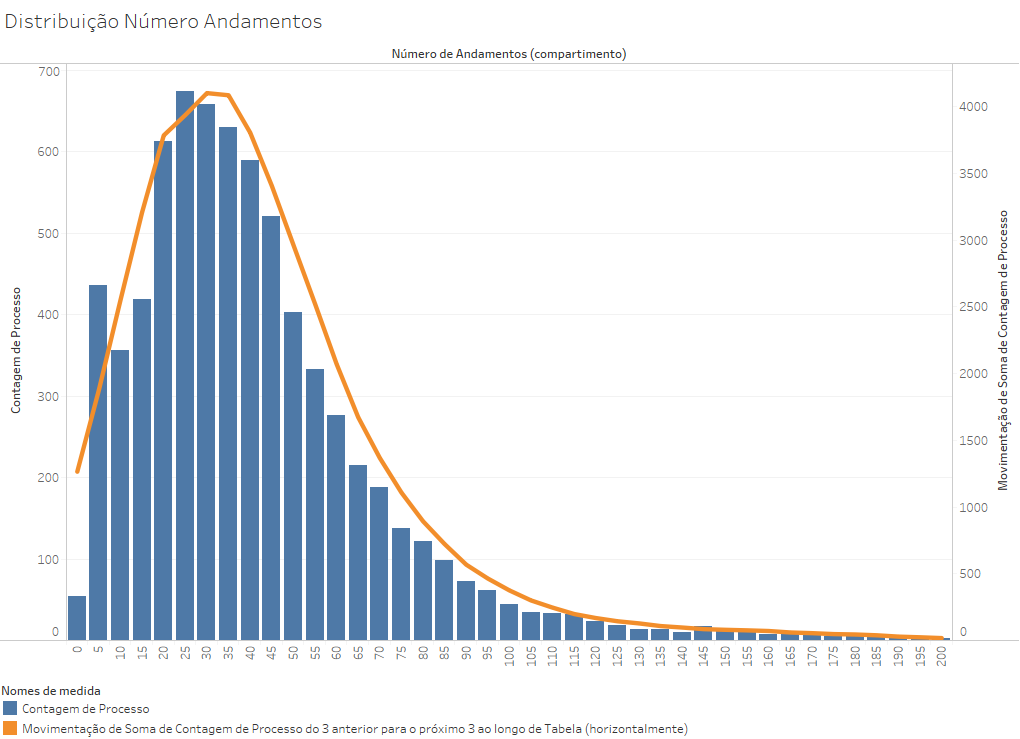
Essa é uma curva de distribuição que não é simétrica, pois ela sobe rapidamente do 0 ao 25 e depois cai gradualmente, com uma longa cauda à direita. Isso acontece porque não há tantos processos com número reduzido de andamentos, visto que eles recebem alguns encaminhamentos no início de sua tramitação que tornam difícil que um processo, por mais rápido que seja o seu encerramento, tenha menos de 5 andamentos.
2.1 Curva normal de distribuição
Os estatísticos perceberam que inúmeros fenômenos naturais e sociais seguem uma curva de distribuição simétrica, em que as caudas à direita e à esquerda são semelhantes. Veja as curvas de distribuição de frequências seguintes:
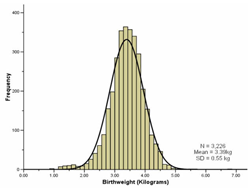
Essa forma com um pico central e curvas simétricas é chamada de curva de sino, e ela é seguida por vários eventos aleatórios. Caso você jogasse 2 dados e anotasse os valores totais, teria uma curva desse tipo, com pico no valor 7 (que é formado por várias combinações de dados), e mínimos em 1 e 12, que ocorrem apenas em uma combinação (1+1 e 6+6).
Gerando lançamentos aleatórios no algoritmo de aleatoriedade do Excel, criamos um gráfico para 1000 lançamentos de dois dados.
No Excel, você pode usar a função ALEATÓRIOENTRE(NúmeroInicial;NúmeroFinal), que retorna um número inteiro aleatório entre dois números inteiros que você defina entre parênteses. O comando ALEATÓRIOENTRE(0;1) retornará um número inteiro entre dois resultados possíveis, sendo o correspondente a um lançamento de moeda. O comando ALEATÓRIOENTRE(1;6) seria o correspondente a um lance de dados, e é ele que usamos para gerar os resultados usados nos gráficos a seguir.
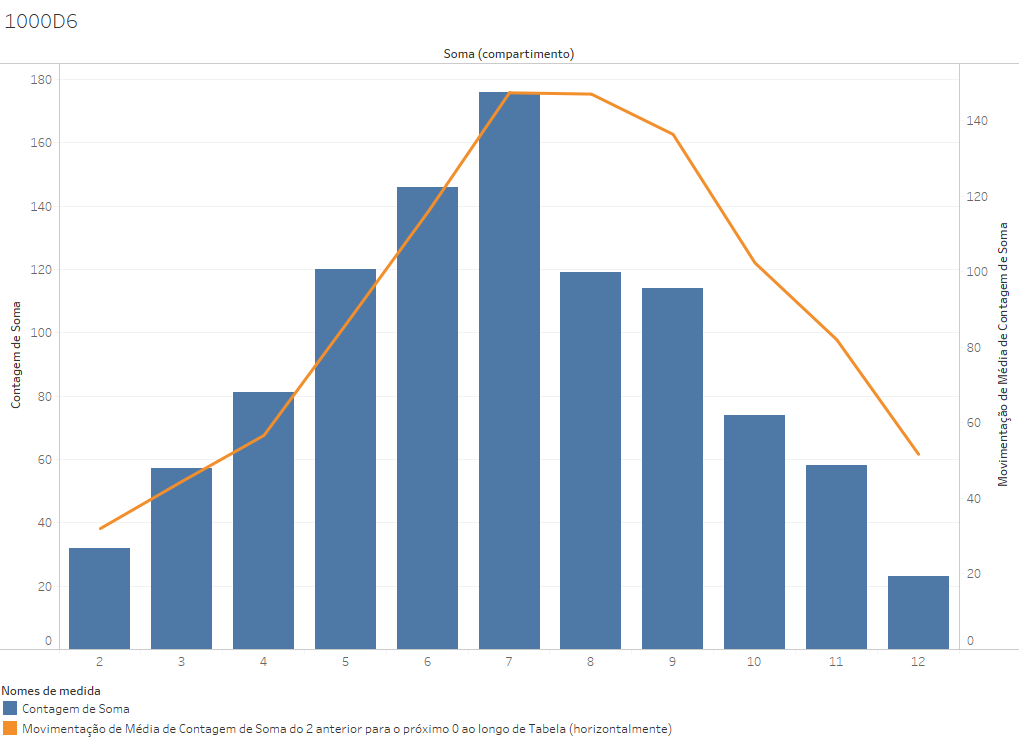
Embora esperássemos uma distribuição simétrica, o resultado foi assimétrico, com mais resultados menores que 7 do que resultados maiores que 7. Por que isso ocorreu? Uma falha do algoritmo? Não. Ocorreu simplesmente porque 1000 lançamentos não é um número grande o suficiente para que possamos contar, com segurança, que a distribuição seguirá, na média, os padrões de uma distribuição ainda maior de eventos aleatórios.
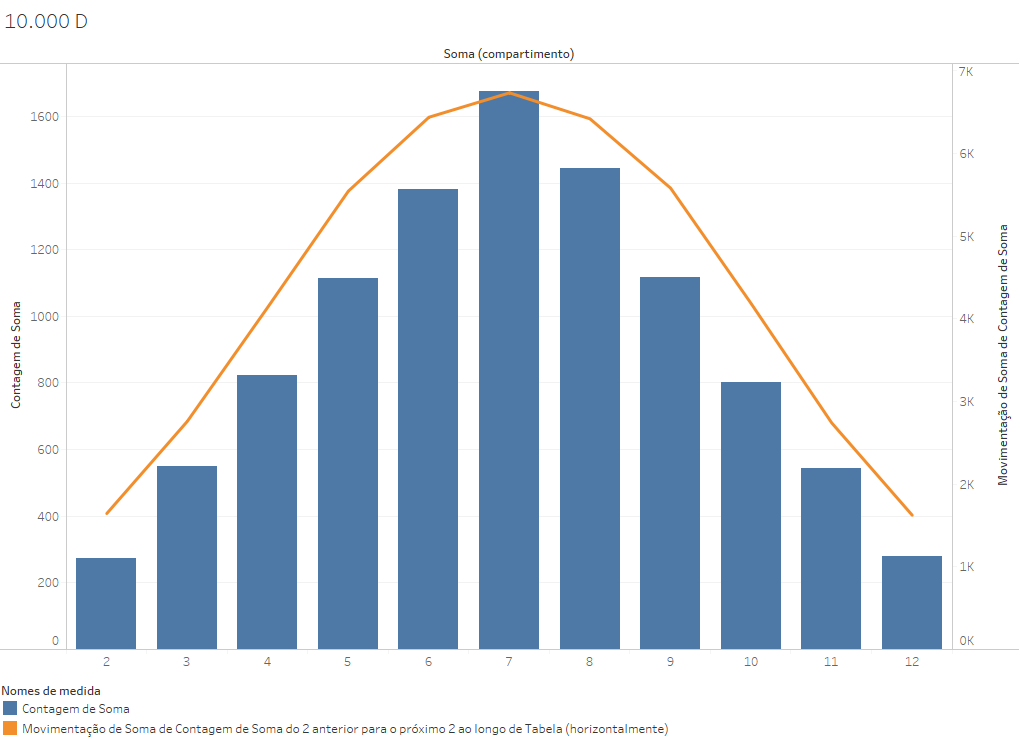
Quando chegamos a 10.000 lançamentos, o resultado é bem mais regular do que com 1000 lançamentos. E com 100.000 lançamentos, será ainda mais regular.
Além disso, a soma de dois dados de seis lados (2xD6) é um evento muito simples, em que a aleatoriedade dos seus elementos não permitem uma acomodação das diferenças. O gráfico de distribuição de uma soma de 4xD6 já oferece uma distribuição mais regular (mas não perfeitamente regular), pela complexidade do próprio evento mapeado. Quanto mais complexo o evento, mais se espera que os elementos que o compõem terminem por gerar distribuições regulares.
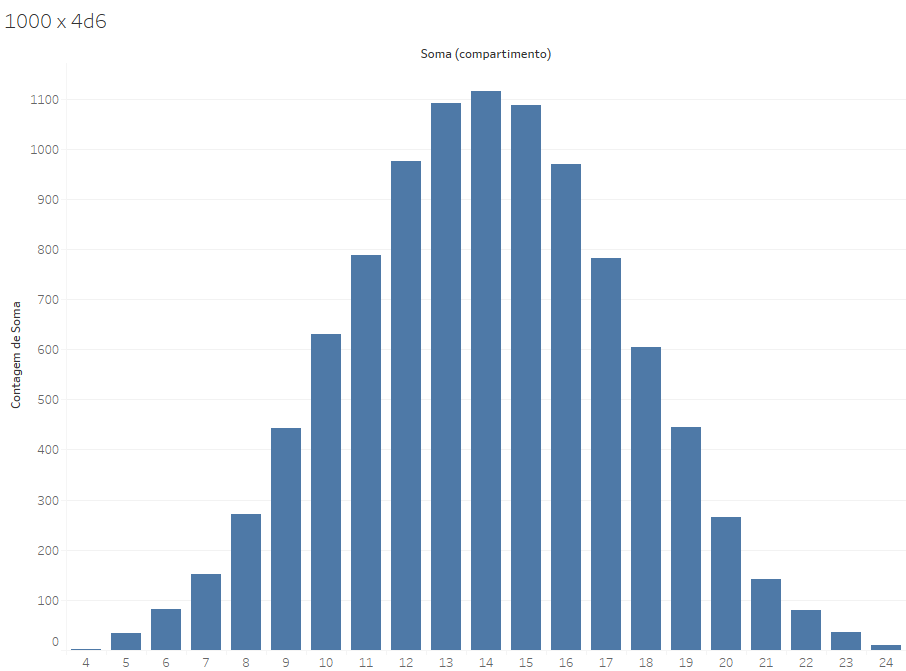
Eventos reais nunca serão totalmente simétricos, mas, seguindo a lei dos grandes números, a distribuição real se aproximará cada vez mais do que se chama de curva normal de distribuição, que é a curva com um sino perfeitamente simétrico, que tem o formato das distribuições que você visualizou acima.
Um ponto que é necessário frisar é que a complexidade dos fenômenos é fundamental para que eles se deixem representar em uma curva normal. Se criarmos uma curva de distribuição de 10.000 jogadas de um D6 (e não da soma de dois dados), o resultado será:
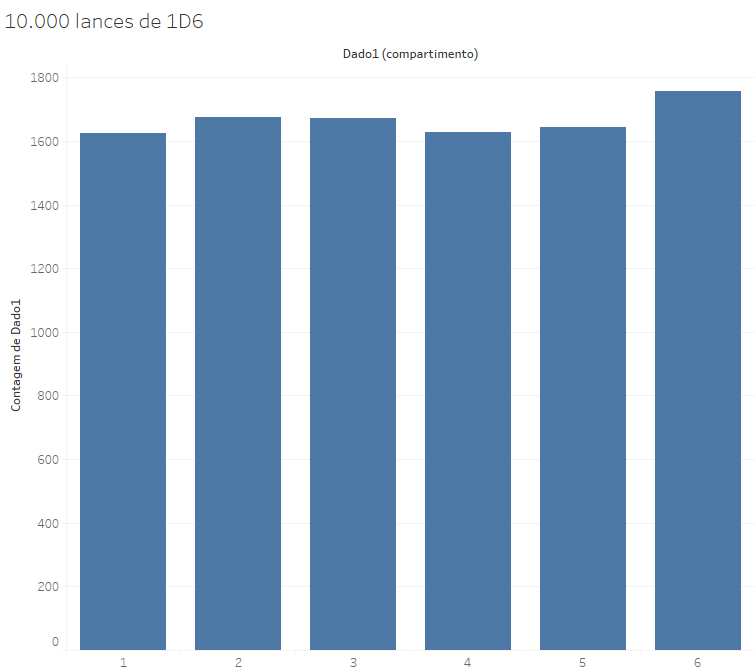
Individualmente, os lances de um dado não são eventos complexos, mas eventos simples, que se distribuem de maneira regular entre as 6 possibilidades. Mesmo 10.000 ocorrências do evento não nos levam a uma distribuição tão próxima das probabilidades calculadas, mas nos levam a números próximos.
Somente quando criamos um evento mais complexo, com 12 possibilidades diferentes de resultados, decorrentes de interações entre eventos aleatórios autônomos (cada lance de dados), é que chegamos a um tipo de evento cuja distribuição segue uma curva normal de distribuição.
Se fizermos 10.000 lançamentos de moedas, distribuição das ocorrências será em duas colunas de tamanhos similares, pois há somente dois resultados possíveis, com chance de 50% para cada um ocorrer. Esse é um evento cuja distribuição não segue uma curva normal. Porém, quando dividimos esses 10.000 lançamentos em grupos de 1.000 grupos de dez lances, e contabilizamos a soma dos resultados (usando 0 para cara e 1 para coroa) o resultado que aparece é diferente: uma distribuição normal.
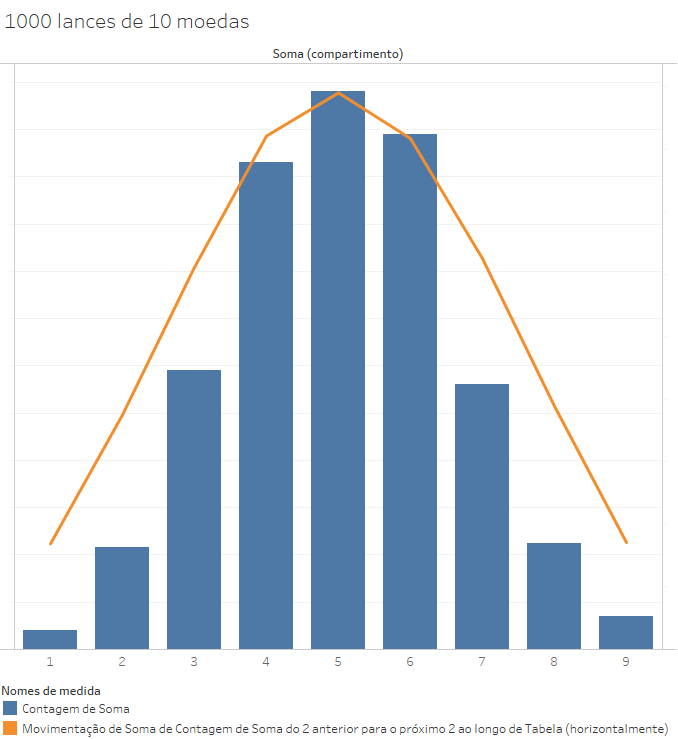
Todavia, se tomarmos apenas os 50 primeiros grupos de lances, o resultado é bem diverso:
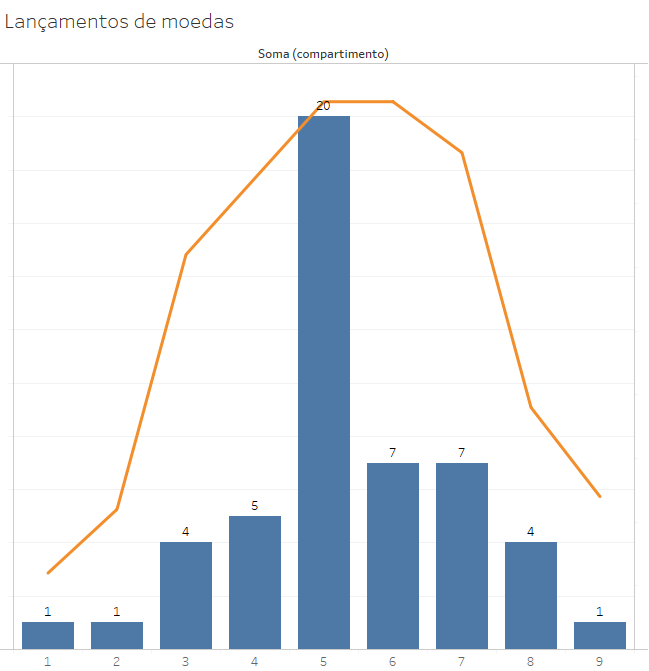
Já os lances de 51 a 100 formam outro padrão:
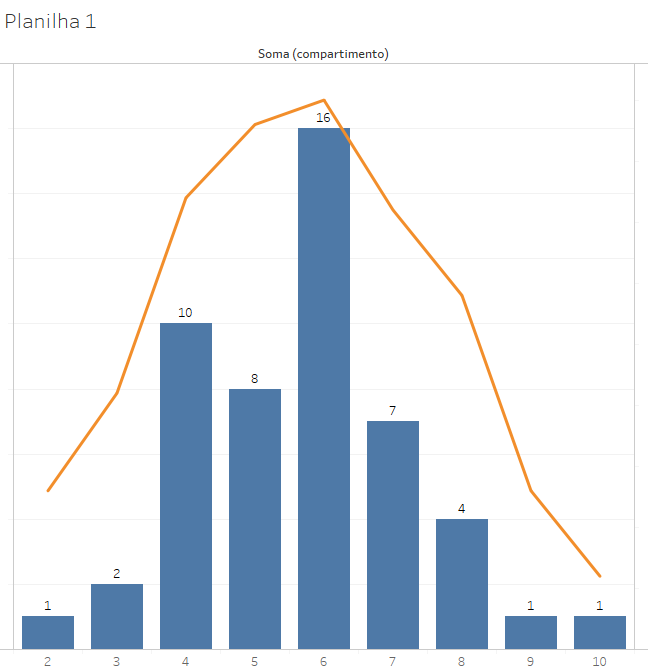
Cada grupo de 50 lançamentos terá distribuições muito diversas, embora o grupo de 1000 lançamentos seja próximo à curva normal. Assim, podemos notar que:
- a população de lances isolados não tem uma distribuição normal, mas uma divisão de aproximadamente 50% de caras e 50% de coroas;
- a distribuição de 50 eventos de lançamentos de 10 moedas não gera uma curva normal, embora seja um evento aleatório,
- 1000 lances de 10 moedas já geram uma curva próxima à normal.
Isso indica que, embora nem os eventos isolados, nem pequenos grupos de eventos tenham uma distribuição normal, a existência de um grande número de eventos pode gerar um padrão definido de distribuição. No caso dos lançamentos de dados e de moedas, há um campo de resultados bem definido (possíveis somas), que são equidistantes do ponto em que se espera maior concentração: trata-se, aqui, de uma curva com um pico no centro uma cauda para cada lado.
Objetos que são formados a partir de uma série de eventos aleatórios que se somam podem compor conjuntos que seguem uma curva normal de distribuição, com relação a uma medida determinada pela agregação de vários fatores. Quando as medidas se distribuem de forma simétrica com relação a um centro (como ocorre no lançamento de dados), essa distribuição segue o padrão que chamamos de curva normal.
Um dos pontos mais relevantes de identificar que um fenômeno segue a distribuição normal é que alguns padrões se repetem nesse tipo de curva: nessa distribuição, o cálculo do desvio padrão (representado pela legra grega σ) permite estimativas seguras sobre a probabilidade de que um certo evento ocorra:
- Cerca de 2/3 (mais exatamente, 68,3%) dos eventos ficam a 1 desvio padrão da média,
- Menos de 5% dos eventos ficam na faixa de dois desvios padrão da média;
- Apenas uma quantidade mínima (0,3%) dos eventos ficam a mais de 3 desvios padrão da média.
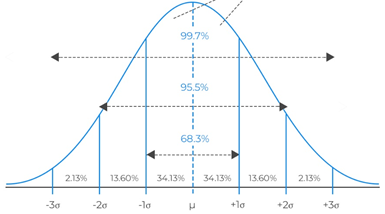
Essa constatação permite o uso do que se chama de regra empírica: em distribuições que se aproximam da curva normal, aplica-se o padrão 99-95-68:
- 99% dos elementos estão a 3 desvios padrão da média;
- 95% dos elementos estão a 2 desvios padrão da média;
- 68% dos elementos estão a 1 desvio padrão da média.
2.1 Curvas de distribuição assimétricas
No caso da distribuição de informações sobre processos, essa curva não costuma ser simétrica (em forma de sino), mas assimétrica (com uma cauda maior para um dos lados), pois as medidas que utilizamos (número de andamentos, número de partes, tempo de tramitação, etc.) costumam estar concentradas no início do eixo, visto que há uma série de processos com julgamento rápido, poucos andamentos e poucas partes.
A distribuição do tempo de tramitação das ações com resultado final próprio (não contamos as que aguardam julgamento nem as que foram apensadas), feita na base Artigo2018 (com ADIs e ADPFs julgadas até 2016), gera o seguinte resultado:
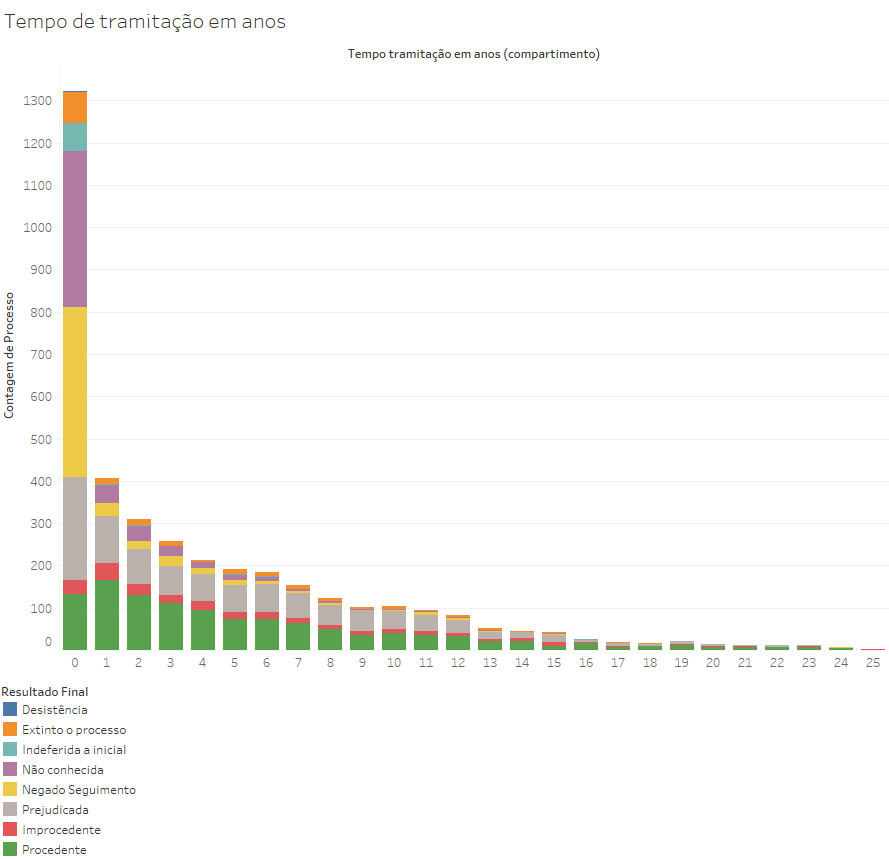
Tal como no gráfico da distribuição do número de andamentos por processo, existe uma concentração no início do gráfico, que você pode notar que se trata basicamente de ações extintas com menos de um ano por motivos processuais (negado seguimento, indeferida a inicial, não conhecimento). Trata-se majoritariamente de ações decididas rapidamente, mas se tornam minoritários nas ações julgadas com mais de 1 ano de tramitação. Já as decisões de procedência são proporcionalmente poucas no primeiro ano, mas tornam-se (juntamente com as prejudicadas) os resultados típicos das ações julgadas com mais de um ano de tramitação.
Em uma situação como essa, não opera a regra empírica. De fato, existe nessa distribuição apenas cerca de 16% de processos fora da distância de 1 desvio padrão (em vez de 32%). E somente 3,5% estão acima de dois desvios padrão, em vez de 4,5%.
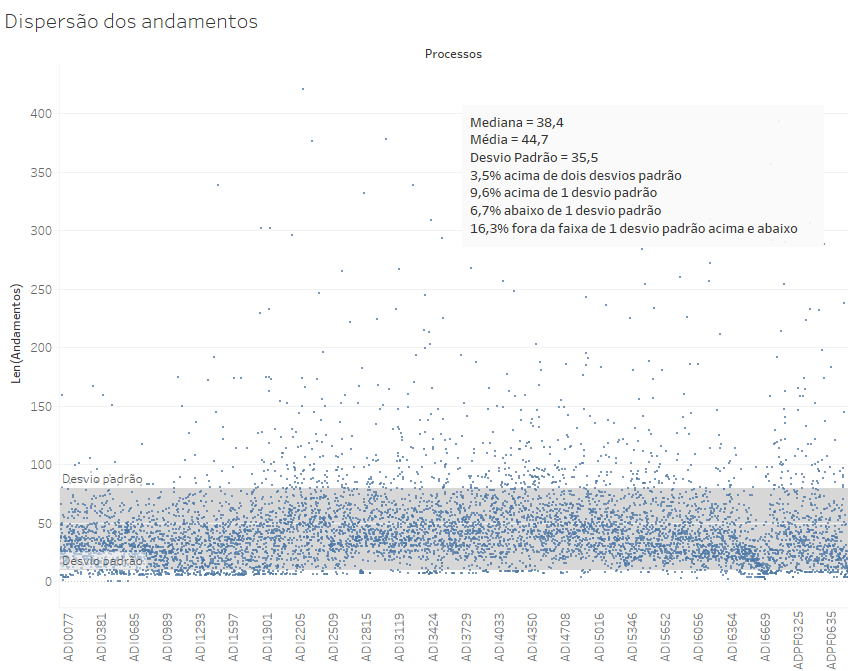
3. Inferência de uma população por meio de uma amostra
3.1 Teorema do limite central
Até este ponto, estivemos no campo da estatística descritiva, que parte do conhecimento de dados de uma população inteira. Tomamos algumas populações, ou alguns recortes dela, e utilizamos alguns gráficos e medidas para entender melhor a distribuição de suas características.
Existem, porém, várias situações em que é inviável fazer um estudo censitário: ou porque não se tem os meios econômicos, ou porque o tempo necessário para o estudo tornaria os resultados irrelevantes. Um caso típico dessa situação é a das pesquisas de intenção de voto: seria demasiadamente caro entrevistar todos os cidadãos brasileiros sobre suas intenções de voto e, mesmo que fosse possível pagar por isso, o tempo para realizar todas essas entrevistas não permitiria que a pesquisa oferecesse um retrato das intenções em um determinado momento.
Quando uma população (por exemplo, o conjunto dos eleitores brasileiros) não pode ser estudada por inteiro. É nesse ponto que passamos para a estatística inferencial, que é o ramo da estatística que trata da construção de conclusões sobre uma população que não conhecemos, a partir de dados colhidos com relação a uma amostra conhecida daquela população.
Outro caso extremamente útil de aplicação da estatística inferencial é a possibilidade de se inferir características de uma “população futura” em uma amostra presente, ou seja, a previsão de tendências - uma tarefa complexa e com limitações, mas possível.
A estatística inferencial fornece uma série de ferramentas para se descrever características da população (chamadas de parâmetros) a partir das características de uma amostra (chamadas de estatísticas).
Mas como é possível inferir parâmetros populacionais a partir de estatísticas baseadas em amostras restritas?
A resposta está na curva normal.
Já vimos que lances individuais de dados não seguem uma distribuição normal. Porém, quando avaliamos grupos de 50 lances de dados, a distribuição já se aproxima da curva normal.
Por que isso acontece? Quando temos várias amostras suficientemente grandes (amostras maiores que 30 já começam a ser suficientes esse tipo de análise), e analisamos uma determinada variável, o valor médio calculado a partir dos elementos que compõem a amostra tendem a ser próximos à média da população. Vamos dar um passo atrás e ver a distribuição de 10.000 lances de 1D6:
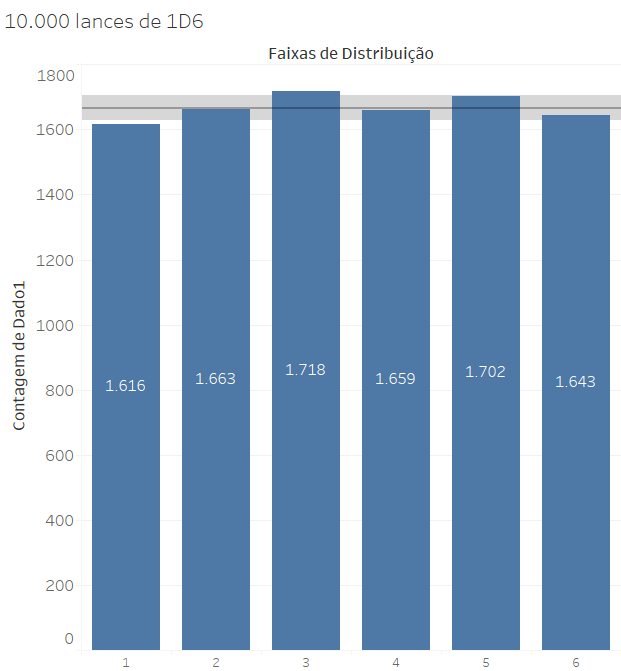
Nesse caso, a média é de 1.667 e o desvio padrão é de 37,6, o que significa que há uma faixa de distribuição bastante estreita com relação à média. Essa não é uma distribuição normal, mas uma distribuição equitativa de 6 resultados diferentes, com igual probabilidade de ocorrerem.
Essa configuração se modifica quando não inserimos o valor individual de 10.000 lances simples, mas o valor de 10.000 eventos mais complexos: lances de 4 dados de 6 lados (D6).
Por exemplo, se observarmos a distribuição dos valores médios de 10.000 lances de 4xD6, o resultado é o seguinte (note que esse gráfico já foi usado acima):
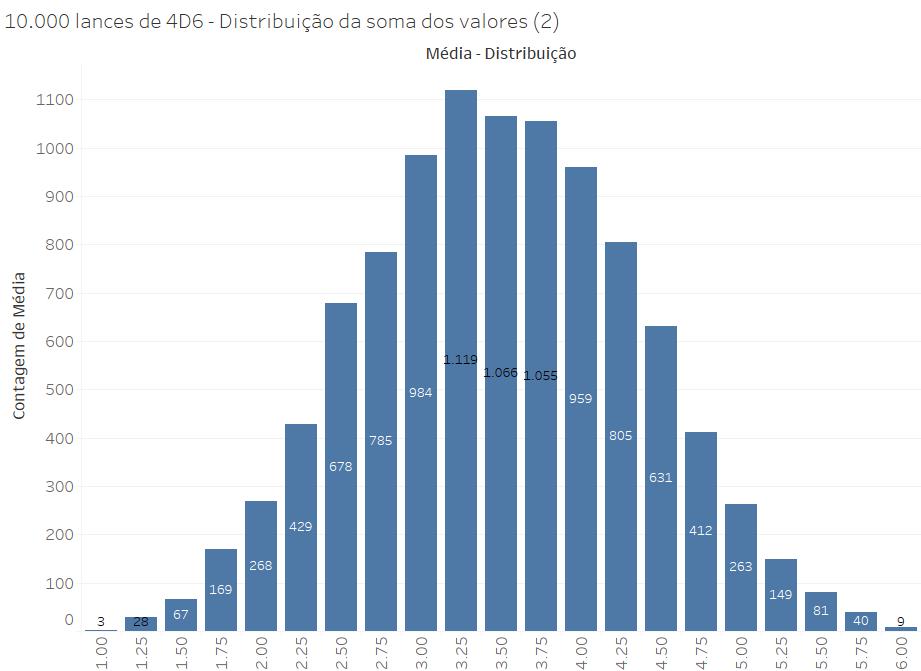
A mesma configuração aparece quando visualizamos as somas, em vez das médias, pois trata-se de uma medida agregada que mapeia exatamente a mesma distribuição, pois a média é a soma dividida por 4:
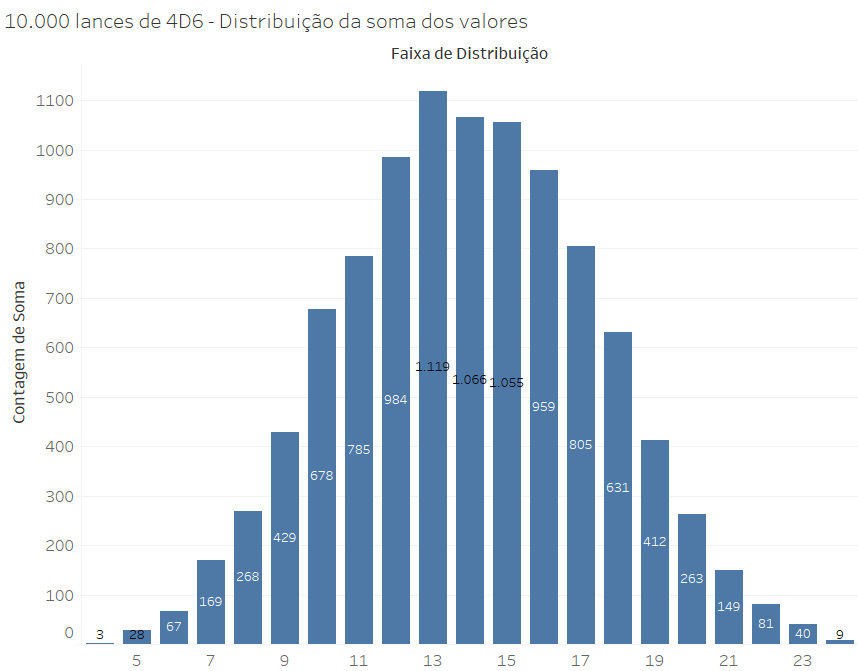
Essa é uma distribuição centrada no valor médio (14, que é a média entre 4 e 20), e que se expande lateralmente na forma de caudas simétricas. Podemos observar o mesmo fenômeno a partir de um gráfico de dispersão, que apresenta um ponto para o valor da soma de cada um dos 10.000 lançamentos:
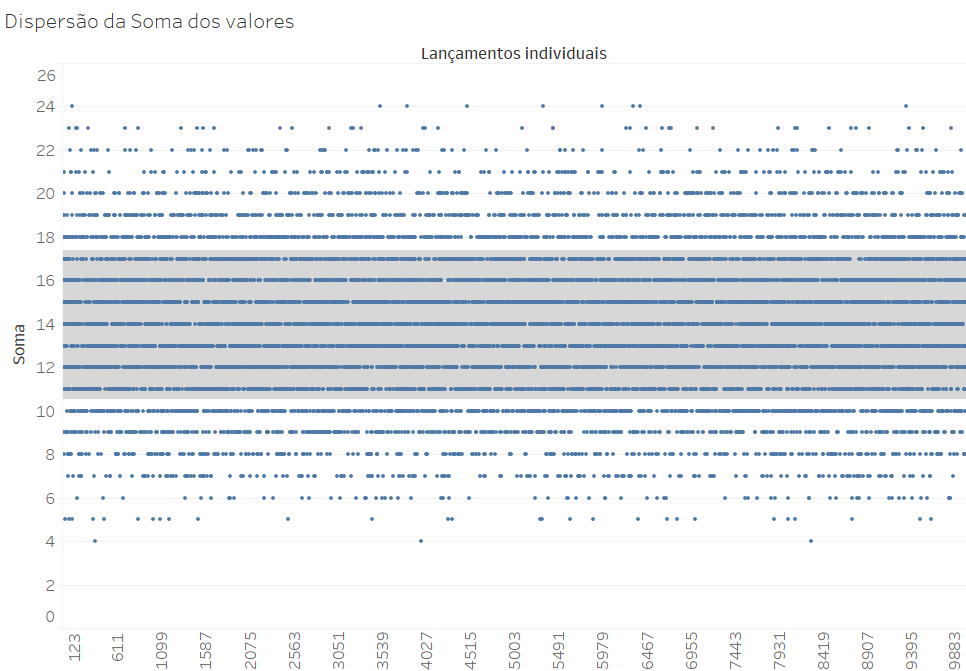
A faixa cinza mostra os limites de um desvio padrão a partir da média (14), sendo que esse desvio padrão é de 3,42. O gráfico acima mostra a dispersão de 10.000 eventos isolados. Porém, quando agrupamos essa população de eventos em 345 grupos aleatórios de 30 lançamentos (nesse caso, sem repetir elementos nos grupos), teremos um conjunto de resultados bem próximos da média:
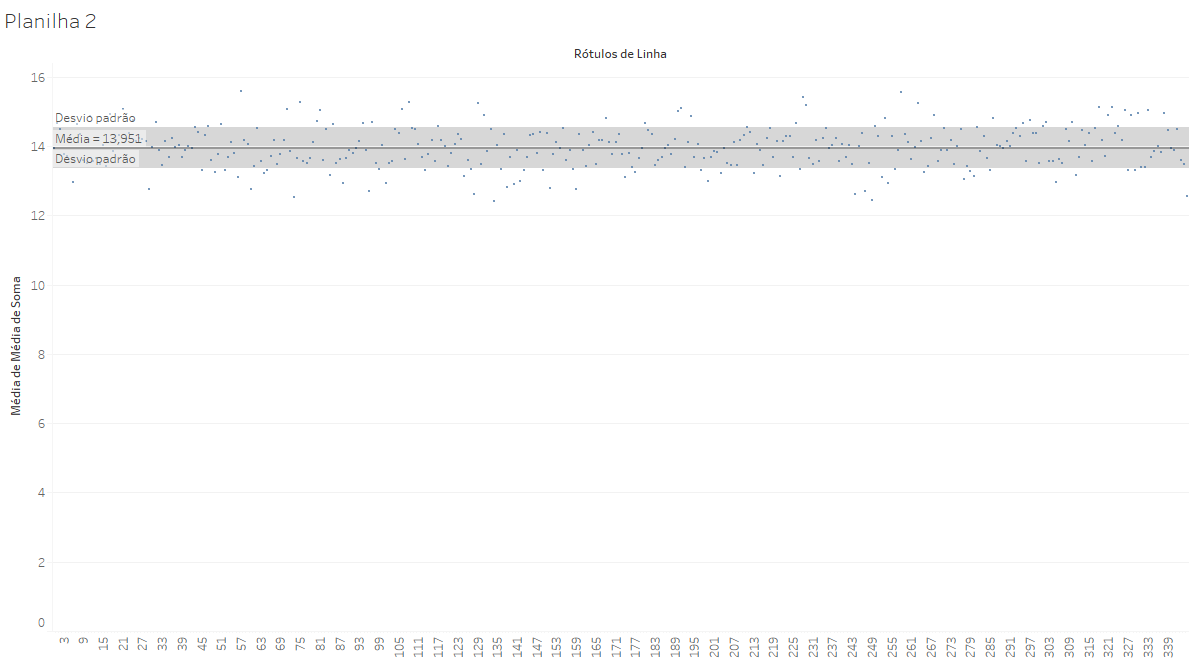
Em vez de resultados entre 4 e 24, as médias de grupos de 30 variam muito menos: entre 12,1 e 15,6, girando em torno do valor médio de 13,978 (que é praticamente o valor médio esperado de 14, ponto médio entre 4 e 24). Nesse caso, o desvio padrão é de apenas 0,64.
O que esse resultado nos sugere é que, em amostras relativamente grandes, os valores das médias amostrais (no caso, a média do valor total obtido em cada lance) se aproximam das médias populacionais.
Em nossos 10.000 lances, o valor máximo de uma média foi de 15,5. É claro que não seria impossível que uma amostra de 30 grupos de 4 lances fosse composto por 120 lances de 6, gerando uma média de 24. Porém, esse evento seria muito raro, tão raro que se tornaria razoável supor que nossas amostras dificilmente alcançariam patamar tão extremo (algo que dificilmente ocorreria, mesmo que você passasse sua vida toda a jogar dados), exceto se lançássemos os dados trilhões de vezes.
Mas não devemos perder de vista que eventos raros ocorrem. Wheelan conta de um homem que foi preso porque o seu DNA correspondia ao DNA identificado como sendo de um homicida, sendo que havia apenas uma chance em um milhão de que esse teste desse positivo para uma pessoa diferente do verdadeiro autor do crime. Se uma pessoa fosse identificada próximo ao local do crime, com circunstâncias que gerassem suspeita, e esse teste desse positivo, seria um argumento sólido para a sua culpabilidade.
Porém, se o DNA atribuído ao homicida for comparado com milhões de DNAs diferentes, em um banco que guarda testes de DNA, é muito provável que sejam identificadas algumas pessoas que têm proximidade suficiente com o DNA do agressor para que gerem um falso positivo. Eventos que ocorrem apenas uma vez em um milhão tendem a ocorrer, de fato, quando ampliamos suficientemente a população analisada.
Por mais raro que seja, tirar uma sequência de 10 resultados 6 seguidos em um jogo de dados (algo que tem uma chance de ocorrer a cada 60 milhões de vezes), se você jogar um dado um bilhão de vezes seguidas (algo em torno de 12 horas por dia, um dado por segundo, ao longo de 60 anos), é bem possível que ocorra uma sequência assim.
Mas uma pessoa com Covid pode ter de um bilhão a 100 bilhões de vírus em seu corpo. Nesse caso, a replicação que gerou esses vírus pode ter pequenas alterações genéticas, tão ou mais raras quanto uma sequência de 10 resultados 6 seguidos. Quando aumentamos suficientemente as ocorrências analisadas, alterações raras se tornam prováveis. Quando temos milhões de pessoas infectadas e um alto índice de contágio, torna-se previsível que algumas variantes surgidas por mutação aleatória terão a oportunidade de infectar várias pessoas e, ao longo do tempo, podem se tornar os patógenos prevalentes em uma população.
Mas voltemos aos nossos jogos de dados. Cada amostra contém 30 conjuntos de quatro lances, dos quais podemos calcular a soma, a média, a mediana ou qualquer outra medida agregada. Cada uma dessas amostras têm uma média própria, com relação a essas medidas: a média amostral, que variou entre 12,1 e 15,6 (para a soma dos valores dos dados).
A primeira coisa a notar é que esse é um intervalo bem mais restrito que a faixa de distribuição de cada lance de 4 dados (que variou de 4 a 24). Mas a observação mais importante é a de que:
os valores das médias amostrais se distribuíram de forma regular, em torno da média populacional.
De fato, quando criamos um gráfico de distribuição desses resultados médios (em 346 amostras de 30 eventos de lances de 4 dados), temos um resultado próximo da curva normal:
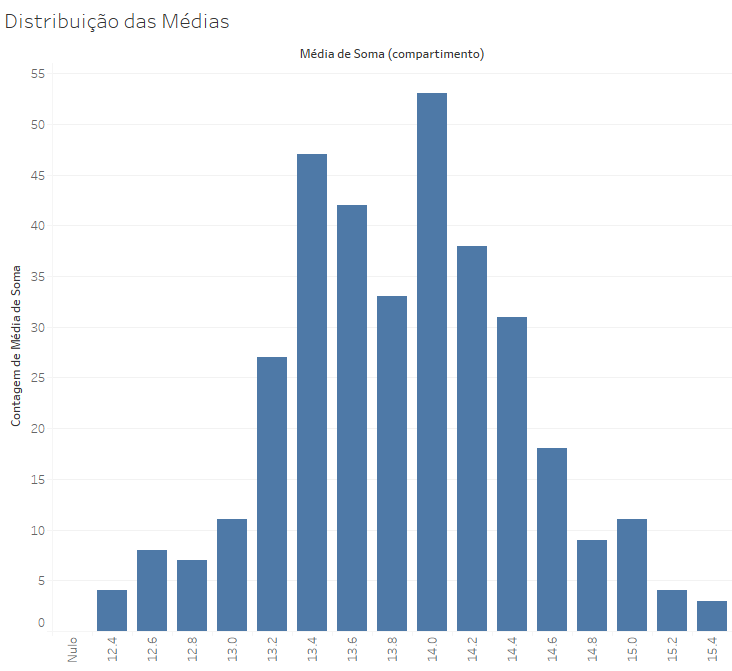
Para amostras, 30 lances é um número relativamente pequeno, que nos oferece valores tipicamente distantes das médias populacionais. Podemos esperar uma proximidade relativa, mas são necessárias amostras maiores para que a distribuição das médias amostrais seja mais próxima à curva normal.
Se elevarmos essa distribuição para amostras de 120 elementos, temos uma curva mais próxima da normal, com um desvio padrão bem menor: ele cai de 0,64 para 0,31.
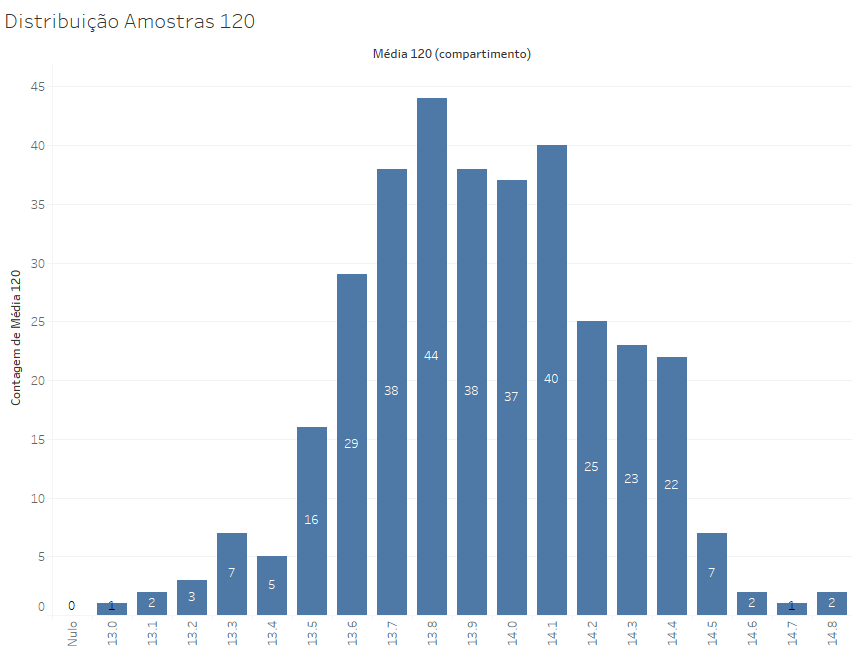
Amostras de 120 lances nos oferecem resultados mais precisos, e se elevarmos essas amostras para 360, teremos resultados ainda mais próximos da média populacional, com um desvio padrão de apenas o,18 e resultados que variam entre 13,4 e 14,4, o que reduz bastante a margem de erro esperada. Nese caso, todas as médias encontradas estão a no máximo 0,6 da média populacional, ou seja, aproximadamente 4% para mais ou para menos.
Portanto, quanto maior for o tamanho da nossa amostra, menor o desvio padrão das médias (chamado de erro padrão) e menor a amplitude em que todas as médias amostrais se encontram. No caso de 300 amostras, é de se esperar 95% de todas as médias amostrais estejam distribuídos na faixa de 2 erros padrão (ou seja, 0,36) acima ou abaixo da média populacional.
Para aprofundar o conhecimento acerca de erro padrão e margem de erro, leia o texto complementar Erro Padrão, Margem de Erro e Z-score.
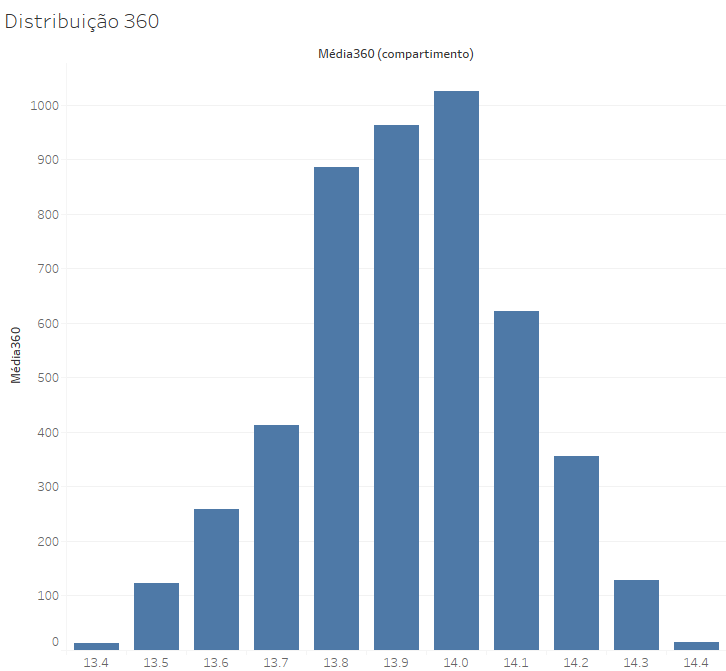
Vemos que o aumento do tamanho da amostra gera resultados cada vez mais seguros, no sentido de que a média amostral tende a refletir a média populacional.
Esse fenômeno nos indica um dos pontos mais importantes da estatística, que é o teorema do limite central:
a curva de distribuição de uma série de amostras segue a distribuição normal!
A importância desse reconhecimento é fundamental porque é justamente o fato de que um conjunto (suficientemente grande) de amostras (suficientemente amplas) segue a distribuição normal nos permite inferir características da população, a partir das características de uma amostra.
Mesmo amostras pequenas (e de fato 30 é o número mínimo aceitável para que comecemos a analisar amostras) nos oferecem alguns elementos importantes para compreender como as médias amostrais se relacionam com as médias populacionais.
A distribuição de amostras de lançamentos de 4 dados nos dá um resultado que aponta de uma curva normal, fato que já é sugerido pelo gráfico das amostras de 30 elementos e que se torna cada vez mais claros quando visualizamos amostras maiores. Isso decorre do fato de que um grupo de 30 (ou 120 ou 360) conjuntos de quatro lances gera interações tão complexas que se torna muito improvável que o valor da média amostral desvie consideravelmente da média populacional. São trilhões e trilhões de combinações possíveis de dados. De fato, são bem mais que trilhões de combinações possíveis, mas falar trilhões parece ter mais impacto do que indicar números bem maiores, como 630.
Toda essa complexidade gera resultados que gravitam em torno do mesmo centro (a média populacional), o que faz com que o resultado da distribuição dessas médias amostrais seja aproximada a uma curva normal de distribuição.
Mesmo que os eventos que compõem as amostras não sigam uma distribuição normal, é de se esperar que a distribuição das médias das amostras siga a curva normal de distribuição!
Essa é a percepção central da estatística: como as médias amostrais se distribuem em uma curva normal, previsões acerca da relação entre as médias amostrais e a média populacional se tornam relativamente previsíveis. Assim, a maioria delas estará a um desvio padrão da média, 95% estarão a dois desvios padrão da média, 99,7% estarão a três desvios padrão da média populacional.
Nesse caso, o desvio padrão a ser calculado não é o desvio padrão da distribuição populacional (que já vimos que é de 3,42), mas o desvio padrão da distribuição das médias amostrais, que é bem menor (que já vimos que é de 0,64). Esse desvio padrão da população de médias amostrais é o que chamamos de erro padrão, e é ele que nos dá a medida para avaliar se uma determinada média amostral está muito longe da média populacional.
Em suma, todo esse trajeto de análise das médias amostrais deve deixar claro que podemos afirmar que os valores de uma amostra determinada estão tipicamente próximos da média populacional, na proporção típica da curva normal:
- 65% das amostras terão um valor médio contido a 1 erro padrão do centro (desvio padrão das médias amostrais);
- 95% das amostras terão um valor médio contido em dois erros padrão;
- menos de 1% das amostras terão uma média mais de 3 erros padrão distantes da média das amostras.
Para amostras suficientemente grandes (quão grandes discutiremos mais tarde), podemos pressupor que uma estatística amostral (valor médio dos elementos que compõem a amostra) está próxima do parâmetro populacional e que o desvio padrão da amostra é semelhante ao desvio padrão da população. Quanto maior a amostra, maior a segurança que teremos para afirmar a proximidade desses valores.
3.2 Das amostras à população
Até aqui, partimos de uma população grande (10.000 lances de 4 dados) e, sabendo a média desses lançamentos e seu desvio padrão, fomos capazes de avaliar se as estatísticas de uma amostra estavam próximas do parâmetro populacional.
Essa, porém, não é a situação usual, porque o típico é que desconheçamos os parâmetros populacionais. Normalmente, levantamos dados sobre uma amostra determinada, sem saber quais são as características globais da população.
Nesse caso, o desafio é responder à pergunta:
Qual é a chance de a nossa amostra representar a população?
Esse procedimento de avaliar em que medida é seguro fazer inferências populacionais a partir de uma amostra é chamado de teste estatístico. Uma série de modelos estatísticos são propostos para realização desse teste, a depender da quantidade de amostras de uma mesma população (dividida em subgrupos relevantes, por exemplo), da quantidade de variáveis (uma, duas ou mais) e do tipo das variáveis em questão (quantitativa, categórica nominal ou ordinal, etc.).
Para realizar testes desse tipo, precisamos inverter a estratégia que usamos no ponto anterior, que tomavam como base uma média populacional conhecida e mostravam que as médias amostrais se distribuíam em torno dela.
Mas também podemos seguir o caminho inverso: uma vez que identificamos uma estatística relativa a uma amostra significativamente grande, sabemos que a média populacional tem grandes chances de estar próxima dessa estatística. Para medir essas chances, também podemos usar as propriedades da distribuição normal:
uma vez identificado o valor médio em uma amostra adequada, podemos inferir que há 95% de chance de que a média populacional desse parâmetro esteja a 2 erros padrão da média amostral (para mais ou para menos).
Como há várias formas de selecionar amostras, de projetar a partir delas um parâmetro populacional e de estimar a confiança que podemos ter em nossas inferências, vários são os modelos estatísticos que podem ser construídos e utilizados pelos pesquisadores.
3.3 Definindo as amostras
Repetimos várias vezes que as amostras precisam ser suficientemente grandes para que possamos afirmar, com relativa segurança, que a média amostral está próxima da média populacional.
Mas quão grande devem ser as amostras, para que possamos fazer afirmações seguras a partir delas?
No caso da pesquisa acadêmica, não é típico que precisemos calcular o grau de confiança que nos oferece uma determinada amostra. O normal é seguir no sentido inverso: o que o pesquisador faz é definir qual é o patamar de confiança necessária para que ele possa fazer afirmações sólidas no seu campo de estudo. A partir dessas definições prévias, ele então define o tamanho da amostra que seria capaz de oferecer respostas significativas.
Não faz sentido você investir tempo e dinheiro na análise de uma amostra que é incapaz de gerar resultados significativos. Por isso, a definição dos critérios de seleção de uma amostra adequada é o início de todo trabalho que é baseado em uma estratégia amostral.
Você pode aprender as fórmulas ligadas ao cálculo do tamanho adequado da amostra, mas isso é desnecessário em nossa abordagem introdutória, pois existem calculadoras que realizam essa operação. Existem formas mais precisas, que partem do desvio padrão da amostra e geram resultados mais precisos (e que podem exigir amostras menores), mas o mais comum é usar uma abordagem que supõe um desvio padrão alto e utiliza apenas três parâmetros:
- Tamanho da população
- Nível de confiança da amostra;
- Margem de erro.
Sugerimos que você use a calculadora de tamanho de amostra oferecida pelo site SurveyMonkey, que oferecer uma interface bem simples para realizar esse cálculo.
Para analisar esses elementos, é melhor começar pelos parâmetros de análise que o pesquisador precisa escolher de antemão: a margem de erro e o nível de confiança.
3.3.1 Margem de erro
Sabemos, de antemão, que nunca podemos ter segurança absoluta de que a amostra representará perfeitamente a população. Existe sempre um elemento que chamamos de erro amostral, que é o erro decorrente de projetar, para a população, médias retiradas de subconjuntos dessa população (ou seja, amostras).
Quanto menor a amostra, maior o erro amostral, pois é maior a possibilidade de que as características da amostra não correspondam às características da amostra. É você que precisa definir o intervalo de erro que está disposto a admitir, sendo que esse intervalo impacta diretamente o tamanho da amostra.
Se você quiser uma amostra para analisar uma população de 100.000 eventos, com grau de confiança de 95% (explicaremos isso a seguir) e com margem de erro de 5%, sua amostra precisará ter, no mínimo, 383 elementos.
Isso significa que você espera que o valor médio de uma variável na população analisada deve estar no intervalo de 5% a mais ou a menos que a média da amostra. Estamos acostumados a essa ideia de margem de erro em pesquisas de intenção de voto, que tipicamente adotam uma margem de erro de 2%.
No nosso exemplo, reduzir a margem de erro de 5% para 2% eleva a precisão dos resultados, mas o custo disso é elevar a amostra de 383 para 2.345, que é mais de seis vezes maior. Por esse motivo, vocês verão que muitas das pesquisas de intenção de voto têm amostras em torno de 2.000 pessoas.
Reduzir a margem de erro dessa pesquisa para 1% exigiria uma amostra de 8.763 pessoas, o que elevaria em 4 vezes os custos da pesquisa. Como a margem de erro de 2% parece aceitável nas pesquisas eleitorais (pois esse é um nível de erro que não altera substancialmente a percepção das pessoas e as estratégias eleitorais dos candidatos), o custo de reduzir a margem de erro tipicamente não vale o benefício.
Nas nossas pesquisas qualitativas sobre processos judiciais, é comum que consigamos alcançar as 400 análises necessárias para obter uma margem de erro de 5%, mas pode ser muito oneroso alcançar os mais de 2.000 casos necessários para uma margem de erro de 2%.
3.3.2 Nível de confiança da amostra
O nível de confiança da amostra é uma medição do quanto você tem de segurança que a sua amostra oferecerá resultados dentro do intervalo da margem de erro.
No caso das pesquisas acadêmicas, o mais comum é que admitamos um erro de 5%, o que equivale a exigir um Grau de confiança de 95%. Isso significa que você pode confiar que, em 95% dos casos, a média obtida a partir da amostra estará dentro da margem de erro.
Portanto, a margem de erro precisa ser lida com cuidado. Nunca temos plena certeza que nossas amostras nos darão resultados dentro da margem de erro. O que podemos ter é uma segurança razoável de que podemos confiar que o resultado estará dentro da margem de erro.
Embora o nível padrão de segurança seja de 95%, você pode querer elevar essa confiança a 99% (o que, convenhamos, é algo bem desejável). Ocorre que isso vem com um custo alto: na nossa pesquisa de população 100.000 e margem de erro de 5%, você precisará de uma amostra de 662 elementos. Assim, elevar de uma segurança boa para uma segurança ótima exige praticamente duplicar o tamanho da amostra.
Nas ciências sociais, também é comum utilizar níveis de segurança mais baixos, no patamar de 90%. Na pesquisa de dados, pode ser menos limitante a necessidade de aumentar as amostras, mas pode ser que você somente consiga fazer entrevistas (no tempo e no orçamento disponíveis) com uma parcela menor da população. No caso que analisamos, uma amostra de 215 pessoas pode ser suficiente para gerar uma confiança de 90%, contra as 278 necessárias para gerar 95% de confiança.
Para muitas situações, pode valer a mena ampliar a amostra para gerar uma confiança mais alta, mas em casos nos quais a possibilidade de ampliar as amostras é restrita, adotar essa confiança menor pode ser razoável.
3.3.1 Tamanho da população
Quanto maior a população, maior deverão ser as amostras que geram resultados confiáveis. Porém, você observará que mesmo populações relativamente pequenas (de 1000 eventos) podem exigir amostras relativamente grandes (de centenas de elementos). Isso ocorre porque as amostras precisam ser suficientemente grandes para que não sejam muito alteradas pela possibilidade de terem elementos muito distantes da média.
Uma amostra de 278 eventos pode ser suficiente para analisar uma população de 1.000 eventos, com relativa segurança e uma margem de erro de 5%. Porém, uma população de 10.000 eventos não exige uma amostra dez vezes maior, mas uma amostra de 370 ocorrências (33% maior). E uma população de 100.000 eventos não exige uma amostra 33% maior, e sim uma amostra de 383 eventos, menos de 4% maior. E a amostra necessária para analisar 1.000.000 de eventos é de apenas 385, que é praticamente a mesma.
A partir desse ponto, não há mais ganhos significativos decorrentes do tamanho da amostra. Assim, se você tiver uma amostra de 400 elementos, poderá fazer afirmações relativamente seguras para populações muito grandes, com margem de erro de 5%.
3.4 Definindo o tamanho da amostra pela relação com o tamanho da população
A relação inversa entre o erro amostral e o tamanho da amostra sugere que devemos optar por amostras tão grandes quanto possível. Porém, você deve ter notado que chega um ponto em que os benefícios do aumento da amostra não valem os custos que incorremos para realizar esse levantamento.
Quando temos uma amostra de 30 processos, a confiança que teremos na capacidade de nos oferecer estimativas adequadas sobre a população é muito reduzida. Porém, calculando a partir da proporção da amostra com a população, precisamos de amostras de no mínimo 141 elementos para ter uma confiança de apenas 80% de que os resultados estarão em uma margem de erro de 5%.
Na academia, essa confiança de 80% é considerada pequena, pois uma vez a cada 5, é de se esperar que a sua estimativa esteja fora da margem de erro. É por isso que utilizamos normalmente o 95% como grau de confiança, mas que é ainda mais desejável um 99% de confiança (especialmente quando você usará seus dados para tomar decisões delicadas). No caso da pesquisa de dados, esse intervalo de 99% não é inacessível, pois muitas vezes podemos aumentar as amostras sem custos muito elevados.
Uma dificuldade especial que temos é que nossas populações são relativamente pequenas, especialmente quando passamos dos processos em geral para as decisões. Porém, quando procuramos relações mais específicas (como tratar dos processos ajuizados por partidos políticos), o universo cai muito de tamanho.
Para universos de apenas 500 processos, a amostra necessária para gerar uma confiabilidade de 99% e margem de erro de 2% é de 447 processos, ou seja, de praticamente 90% da população. Nesse ponto, é melhor fazer uma pesquisa censitária, pois o custo de analisar todos os processos termina sendo muito próximo de escolher uma amostra. Mesmo se aumentarmos a margem de erro para 5%, teremos uma amostra de 286 processos, que é mais de metade da população.
3.5 Redução das amostras para populações mais homogêneas
A distribuição acima é calculada com uma hipótese rigorosa, de que as características a serem medidas (por exemplo, a percentagem de processos julgados procedentes) têm uma chance de 50% de ocorrer em determinado processo.
Em outras palavras, esse cálculo parte do pressuposto de que, para cada processo, há uma chance de 50% de ele ter sido ou não julgado. Essa é uma suposição que usamos quando não conhecemos a população analisada e, por isso, pressupomos o máximo de heterogeneidade.
Todavia, para populações relativamente conhecidas, podemos calibrar nossos modelos, introduzindo um índice de homogeneidade, que é descrito de forma bem didática na seguinte Calculadora de Amostragem do site Prática Clínica. Ela permite que você insira elementos de homogeneidade: o nível máximo que se espera de prevalência populacional de uma característica medida e o nível mínimo de prevalência que é possível esperar dela.
Se você estiver lidando com processos judiciais, o nível máximo que se pode esperar de decisões de procedência não é de 50%, mas é tipicamente menor. Inserir esses elementos de homogeneidade (ou seja, de limites para a distribuição de certas características) gera uma redução das amostras necessárias e também um incremento na significância estatística das amostras analisadas.
3.5 Pesquisa de intenção de voto XP/Ipespe 21 a 29 de março 2021
Para avaliar se você compreendeu os elementos deste texto, um exercício interessante é avaliar a pesquisa de intenção de voto XP/Ipespe 21 a 29 de março 2021, sobre as eleições presidenciais de 2022. Na página 48 do relatório contido no link acima, estão as explicações metodológicas envolvidas na pesquisa.
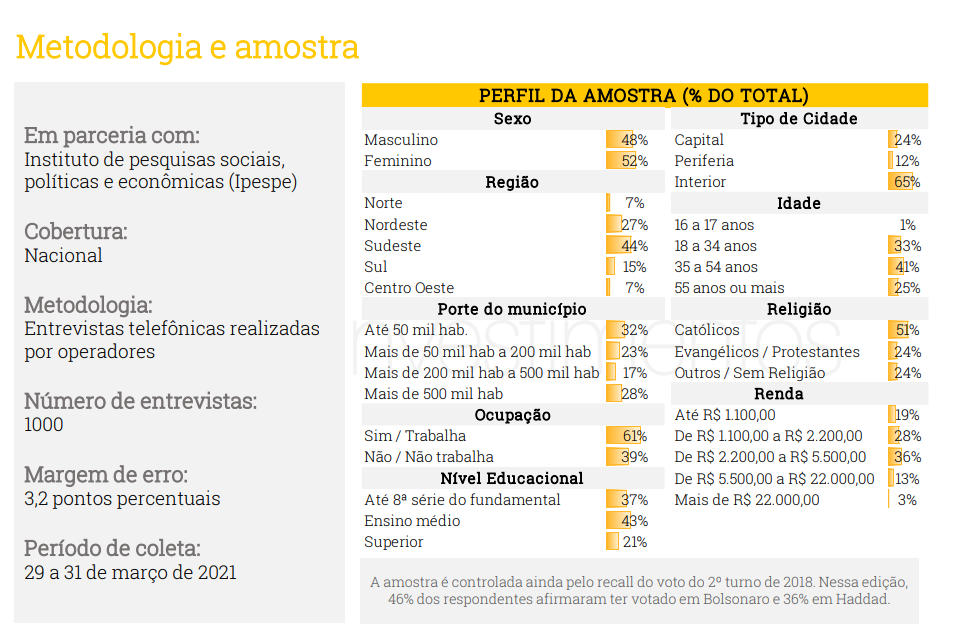
Essa pesquisa indica que foram realizadas 1000 entrevistas, por contato telefônico, e que a margem de erro é de 3,2 pontos percentuais. Com base nos elementos tratados neste texto, você considera que esse número de entrevistas é suficiente para oferecer resultados confiáveis, com essa margem de erro?
Primeiro, tente chegar a essa conclusão de forma autônoma, antes de seguir adiante.
- Se você tentou utilizar uma das calculadoras de tamanho de amostra, deve ter notado que falta um parâmetro de análise: o nível de confiança. Essa ausência deve ser interpretada como a utilização do nível padrão, que é de 95%. Se fosse usado outro nível, ele provavelmente teria sido indicado nesses parâmetros metodológicos.
- Ao inserir a margem de erro, você pode ter tido resultados estranhos. Nesse caso, observe que a notação das calculadoras é a mais típica em nível internacional, que usa pontos como delimitador da parte fracionária, e não vírgulas, o que fará com que o numeral "3,2" seja interpretado como "32". Para definir adequadamente a margem de erro, é preciso colocar "3.2".
- Se você inserir nas calculadoras o nível de confiança de 95% e a margem de erro de 3.2%, precisará estimar a população. Um número razoável para começar seria o total de eleitores no Brasil, que é próximo de 150.000.000 e, nesse caso, o resultado será de 938, que é bem próximo das 1000 entrevistas feitas pelo Ipespe. De fato, se você inserir a margem de erro 3.1, terá exatamente as 1000 entrevistas como amostra mínima. E se você tentar 3.0, terá 1068 como tamanho mínimo da amostra, o que seria maior que o número de entrevistas realizadas.
- Observe também que aumentar a população não altera o número de entrevistas, pois esse patamar já é suficiente para alcançar resultados com 95% de confiança e 3.2% de margem de erro em uma população de qualquer tamanho. E, de fato, esse tamanho de amostra não seria menor caso você buscasse estimar com segurança os parâmetros de uma população de 1.000.000 de eleitores.
- Se você reduzir o tamanho da população para apenas 30.000 eleitores, a amostra necessária será de 910 pessoas, que é um número muito semelhante. Portanto, uma pesquisa eleitoral custa basicamente o mesmo preço seja para federais, estaduais ou mesmo de municípios de médio porte.
3.6 Pesquisa em universos pequenos
Mesmo que você deseje fazer estudos acerca de populações relativamente pequenas (contadas nas centenas e não nos milhares), isso não poderá ser feito de forma segura com amostras proporcionalmente pequenas.
Mas o que ocorre se você pretende fazer uma pesquisa sobre um universo de 200 processos? Nesse caso, a sua amostra precisará ser uma parcela muito substancial do universo pesquisado. Se você considera aceitável uma margem de erro de 5%, terá de analisar 132 processos. Mas, se você desejar uma margem de erro menor, de 2%, terá de analisar 185 processos, o que representa praticamente o mesmo trabalho de realizar um estudo censitário.
Isso indica que a estratégia de fazer estudos amostrais pode não ser a mais adequada quando você tem universos pequenos ou quando você não tem possibilidades práticas de levantar dados sobre uma amostra significativa. Isso pode ocorrer seja por razões de custo ou pela necessidade de cumprir prazos que inviabilizariam esse tipo de trabalho.
Porém, se você já tinha disponibilidade para levantar dados sobre algumas centenas de processos, pode fazer estudos amostrais sobre populações relativamente grandes. Essa investigação pode ser feita com um grau suficiente de confiança, já que um estudo feito com 400 processos pode ser suficiente para tirar conclusões significativas (com 95% de confiança e margem de erro de 5%) para populações de 1.000.000 de processos. E isso se aplica ainda que a amostra somente ofereça resultados confiáveis com erro de 2% para populações de 480 processos.




