No texto Estatística descritiva: principais conceitos, são trabalhados conceitualmente alguns tópicos, que serão explorados de forma prática por meio do software Tableau Desktop.
1. Baixando e instalando o Tableau
Optamos por utilizar o software Tableau Desktop para a realização das análises dos dados e para a formulaçã0 de gráficos. Trata-se de um software profissional, com amplas possibilidades, e que usamos por ser gratuito para estudantes.
Ele pode ser baixado neste link e sua primeira instalação dá direito ao uso gratuito por 14 dias. A empresa fornece licenças gratuitas para estudantes, por meio do preenchimento do formulário que está no final da página Tableau para Estudantes.
Você pode baixar e instalar o Tableau e ativar o período gratuito de teste, enquanto providencia o pedido da licença especial para estudantes, que costuma ser liberada bem rápido.
2. Carregando uma base de dados
Uma vez que os programas estiverem instalados, você deve abri-lo e carregar a base de dados com a qual trabalharemos.
Pela minha experiência, a melhor forma de importar dados para o Tableau é partir de planilhas do Excel (.xlsx). Já tive dificuldades em importar dados diretamente de arquivos .csv, quando há vírgulas dentro dos campos (o que ocorre quando gravamos listas dentro de uma das células). É possível contornar essas dificuldades, mas creio que é mais garantido abrir o arquivo no Excel, salvá-lo como arquivo do Excel (.xlsx), e depois abrir esse novo arquivo no Tableau.
Cuidado! O Excel é útil, mas tem limitações que fazem com que seja preciso tomar um cuidado especial. O Exce tem um limite de 32,767 caracteres por string gravada em uma célula. Isso é suficiente para a maioria dos usos, mas essa quantidade é insuficiente para conter os dados de andamentos das ações com algumas centenas de andamentos, como a ADPF0101, que tem mais de 90.000 caracteres em seus andamentos, o que leva a um erro na abertura dos dados pelo Excel, que não apenas trunca os caracteres contidos na célula, mas gera erros de leitura nos valores seguintes da mesma linha.
Vamos começar nosso exercício com uma base gerada a partir dos dados das ADIs e ADPFs, e que é fruto do Gerador Intermediário de CSV. Estes dados estão disponíveis no Github, no arquivo ADIcsv.xlsx. Notem que existem neste repositório dos arquivos de dados, que foram divididos porque o tamanho total supera os limites do Github. No arquivo indicado, estão todos os dados, menos os andamentos (cuja complexidade demanda outras formas de abordagem e que, por isso, foram disponibilizados em um arquivo específico, no mesmo repositório).
Atenção: os gráficos que você elaborar podem ter valores ligeiramente diferentes das imagens e videos deste texto, pois no GitHub sempre disponibilizo a versão mais nova da tabela, que incorpora melhorias no Gerador de CSV do Acompanhamento Processual do STF e também as extrações mais recentes feitas com o Extrator de dados do Andamento Processual.
Quando você abrir o TableauDesktop, terá uma janela como esta, na qual você deve escolher conectar a um arquivo Microsoft Excel.
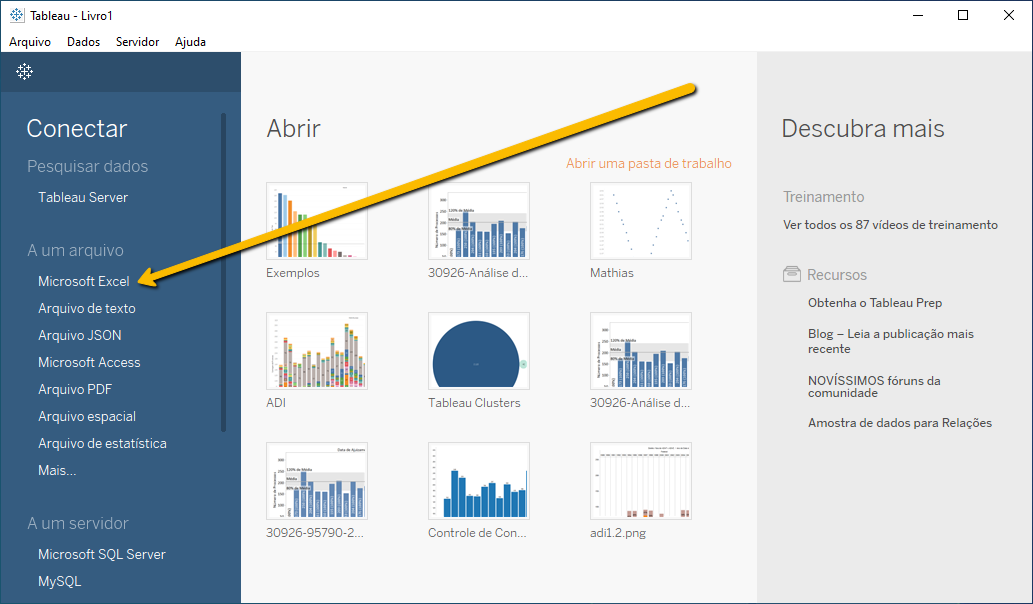
Uma vez que você escolha o arquivo em que você gravou a base de dados contida no GitHub, você terá a seguinte janela, que é a da Fonte de Dados do arquivo do Tableau.
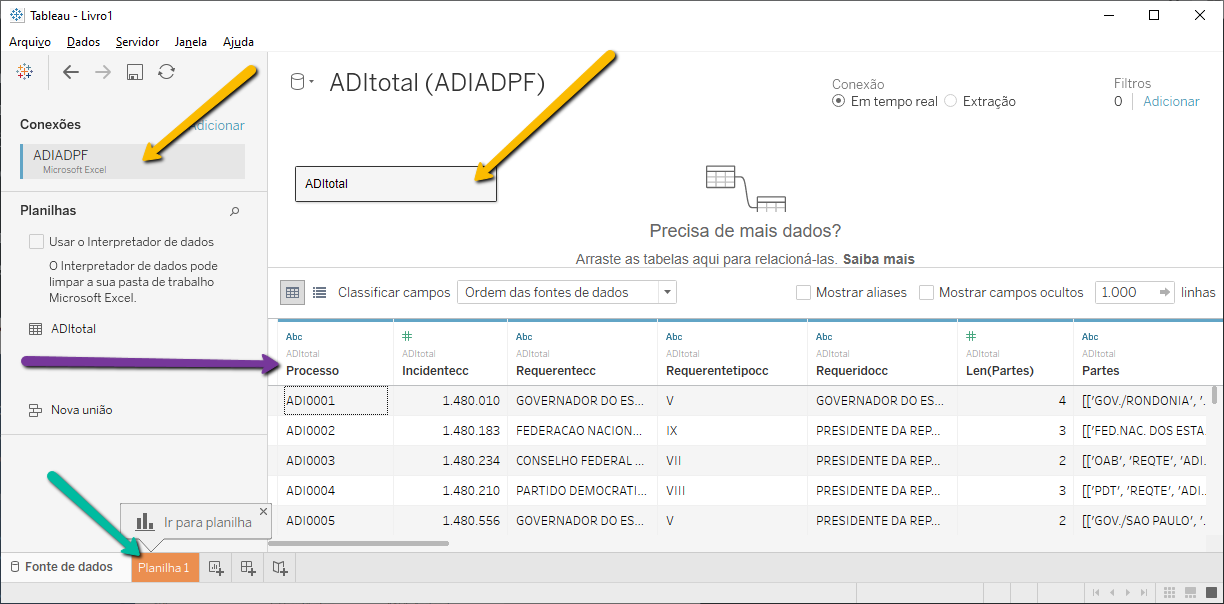
Nesta janela, as setas laranjas mostram qual é o arquivo cujos dados foram carregados (Conexão) e qual foi a planilha carregada deste arquivo do Excel. Como este arquivo tem apenas uma planilha (ADItotal), ele é automaticamente carregada na área de tabelas (segunda seta laranja). Caso o seu arquivo tenha várias planilhas, você precisará escolher quais tabelas deverão ser carregadas e indicar como as tabelas podem ser conectadas por um campo comum (como o nome do processo ou o incidente).
3. Criando gráficos
Uma vez que os dados sejam carregados, você pode apertar o botão "Planilha 1", no canto inferior esquerdo, em que o próprio Tableau indica que você pode "Ir para a planilha", o que vai retirar você da aba de "Fonte dos dados" e abrir a primeira Planilha, nome que o programa dá para cada uma das abas em que você cria um gráfico. A tela que se abre precisa ser bem compreendida para que você siga adiante.
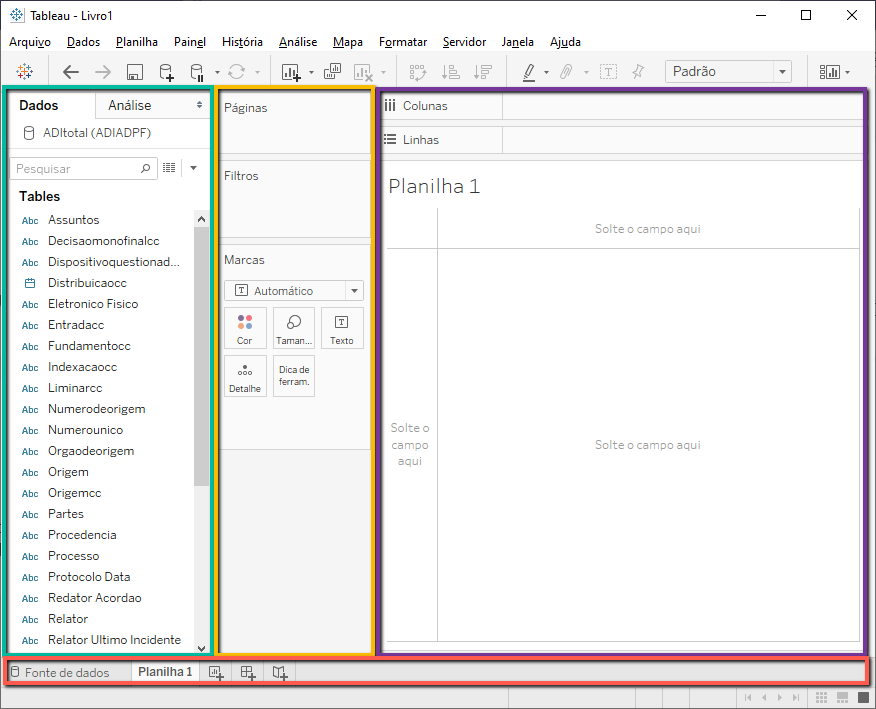
- Painel de campos (Verde). Na janela com os campos, você verá todos os campos, ou seja, os nomes das colunas da tabela. Para criar gráficos, basta você arrastar os campos e soltá-los na parte em roxo.
- Painel de visualisação (Roxo). Essa é a parte em que você poderá visualizar os gráficos, que serão criados na medida em que você selecione variáveis no Painel de Campos e as coloque nas linhas ou colunas, o que você pode fazer diretamente nos eixos do gráfico (nos Solte os campos aqui), ou na parte de cima do painel (nas áreas chamadas linhas ou colunas).
- Painel de filtros e marcas (Amarelo). Nessa área intermediária, você fará ajustes no gráfico, seja criando filtros (que definem os elementos que devem ser incluídos/excluídos) ou criando marcas (ou seja, definindo os vários elementos gráficos que deverão aparecer, especialmente os textos a serem exibidos e o significado dos tamanhos e das cores de cada elemento.
Vamos analisar cada um desses elementos com mais detalhe, mas antes disso vamos criar o nosso primeiro gráfico, pois essa é uma abilidade que se desenvolve por meio da ação. Siga as instruções do parágrafo seguinte, que são ilustradas pelo video subsequente.
Na lista de campos, escolha o campo processo (que é uma string, marcada pelo símbolo 'Abc' azul), e coloque-lo nas colunas, ou seja, no eixo X (horizontal). Depois, baixe um pouco a barra lateral do painel de campos e procure a variável Len(Partes), que é um número inteiro (símbolo '#" verde) que indica o número de partes que o processo tem (envolvendo requerentes, interessados, advogados e amici curiae). Arraste esse campo para as linhas (e veja que não há mais o espaço 'Solte o campo aqui', no painel de visualização.
No final do video, você deve ter notado que escolhemos o ajustar largura, para que o gráfico seja dimensionado de acordo com a largura de tela existente. Escolhemos essas duas variáveis como nosso primeiro exemplo porque elas nos dão a combinação mínima para um gráfico: uma variável categorial (chamada no Tableau de dimensão) e uma variável numérica (chamada no Tableau de medida).
Olhando novamente o painel de campos, você notará que primeiro aparecem as dimensões (com símbolos em azul) e depois vêm as medidas (com símbolos em verde). Se você usar apenas dimensões, não haverá medidas e, por isso, você não poderá fazer gráficos.
Para explorar mais um gráfico, uma boa estratégia é duplicá-lo, para que as modificações feitas não alterem o gráfico original. Você pode duplicar o gráfico clicando sobre o nome da planilha com o botão direito do mouse e escolhendo "duplicar", o que cria uma Planilha 2, com as mesmas características.
O esse gráfico nos diz? Ele nos sugere que as ADIs mais antigas têm um número mais restrito de partes e que, a partir de certo momento, tornaram-se mais comuns ações com um grande número de partes, o que provavelmente se explica por um grande número de amici curiae, que não eram previstos nos primeiros anos de vigência da CF-88.
Porém, não devemos perder de vista que nossos dados não estão classificados por data de ajuizamento, mas por ordem alfabética: primeiro as ADIs, depois as ADPFs. Elas seguem uma ordem relativamente cronológica porque o número das ações segue, grosso modo, a data de protocolo.
Então, vamos fazer uma alteração que nos dará um tipo de gráfico que se repetirá várias vezes em nossas análises: um gráfico baseado em uma data, neste caso, a data de ajuizamento. Nos nossos campos, há algumas datas, e uma das mais completas e confiáveis é a data de protocolo (Protocolo Data).
Mas temos um problema! Veja que a data de protocolo foi lida como uma string (Abc) e não como uma data, o que exige que nós alteremos o tipo de dado, para que a agregação por data possa funcionar corretamente. Clique com o botão direito do mouse sobre o campo Protocolo Data, e mude o tipo de dado para Data. Então, retire do gráfico o campo Processo (arrastando-o para fora) e coloque o campo Protocolo Data em seu lugar, como no video abaixo.
No vídeo, você pode ver também que é possível alterar o campo de data, agregando as datas por dia, ano, trimestre e outras formas de agregação, e que é adequado modificar o modo de lidar com o número de partes. Antes, como havia um número de partes específico para cada processo, não fazia diferença se usássemos soma, média, mediana ou outro cálculo. Porém, no nosso novo gráfico, há vários processos a cada ano, de tal forma que a melhor medida para usarmos nesse caso é a média de partes por processo, no ano, e não a soma do número de partes (como estava no início, o que gerava números difíceis de se comparar).
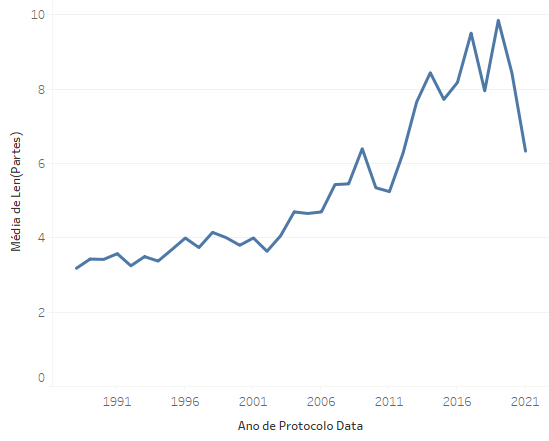
Esse já é um gráfico que nos possibilita ver com mais clareza que, de fato, o número médio de partes aumentou de forma significativa ao longo do tempo, atingindo o ápice em 2019 e depois caindo em 2020 e 2021, o que pode ter alguma relação com a pandemia. Note que a imagem do gráfico acima dificulta um pouco saber que ano corresponde a cada pico, mas essa informação fica clara se você explorar o gráfico no tableau com o mouse, essas informações são dadas para cada ponto. Além dessa possibilidade, o video abaixo mostra como você pode usar o menu "Mostre me" para testar algumas exibições alternativas dos mesmos dados.
Apesar dos testes, o fato de haver uma série temporal faz com que esse gráfico de linha seja normalmente o mais indicado para transmitir, de forma clara e direta, o significado do gráfico.
Para compreender melhor os dados, você pode inserir nele um novo painel, chamado Resumo, que traz algumas informações relevantes para a compreensão do gráfico.
3.1 Média e desvio padrão
No video anterior, usamos o menu de análise para inserir a média, lembrando que se trata da média anual do número de partes dos processos ajuizados. Como se trata de uma agregação anualizada, existem apenas 34 ocorrências e se espera que a existência de valores aberrantes seja diluída pelo grande número de registros agregados a cada período. No final do vídeo, mostramos como inserir a média (clicando duas vezes sobre o Linha Média no menu Análise), sendo que o valor da média está no quadro Resumo.
Uma medida bastante ligada à média é o desvio padrão, que indica quão distantes os valores, em geral, estão da média. Para que isso fique claro, podemos usar o comando Inserir Faixa de Distribuição para agregar ao nosso gráfico uma faixa que mostre como opera um desvio padrão para cima e para baixo da média. Aproveitaremos para retirar a indicação de um valor nulo, pela sua exclusão do gráfico (com o botão direito do mouse).
O resultado é um gráfico importante, pois o que o desvio padrão faz é criar uma faixa indicando que a maioria dos pontos no gráfico está dentro de um desvio padrão da média. Como se trata da média da distância de todos os pontos com relação à média, ao menos metade dos pontos deve estar dentro desta faixa. Neste caso, em que não há valores muito extremos, cerca de 2/3 dos pontos estão dentro dessa faixa de 1 desvio padrão.
Para entender melhor o desvio padrão, é melhor visualizar o gráfico na forma de pontos e nãe uma linha, visto que o desvio não depende da sequência temporal indicada pela linha azul, mas apenas da distância média entre os pontos e a linha média. Quanto menor o número de pontos muito distantes da média, menor será o desvio padrão e, com isso, menor a faixa de distribuição em torno da média necessária para conter a maioria dos elementos.
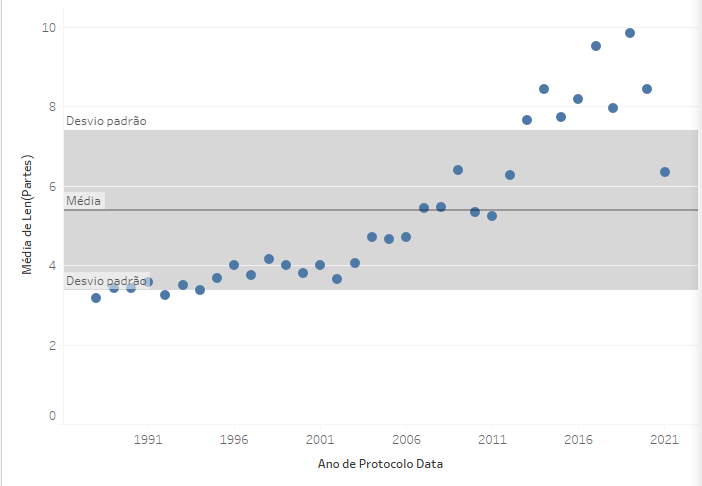
Neste caso específico, percebe-se que há poucos pontos com mais de um desvio padrão para baixo, muitos pontos próximos da média e alguns pontos relativamente acima da distância de um desvio padrão da média. Existe aqui uma dispersão, mas percebe-se que ela é limitada. Os maiores valores são de cerca do dobro da média e os menores valores são de cerca de 60% da média, o que representa uma faixa relativamente estreita de distribuição.
Outra forma de compreender o desvio padrão é observar o que ocorre quando criamos uma faixa de dois desvios padrões, em vez de um, o que pode ser feito editando a faixa do dsevio padrão, clicando com o botão direito do mouse sobre ela.
Dentro de uma população com distribuição relativamente uniforme, essa faixa de dois desvios padrão (ou seja, de pontos que são duas vezes mais distantes do centro do que a média dos pontos) tende a ser pequena. No caso analisado, a faixa de dois desvios padrão engloba cerca de 95% dos elementos, o que deixa de fora apenas os valores mais extremos, para cima e para baixo (nesse caso, apenas para cima). Neste caso específico, mesmo os valores mais altos estão bastante próximos do limite superior desta faixa de distribuição.
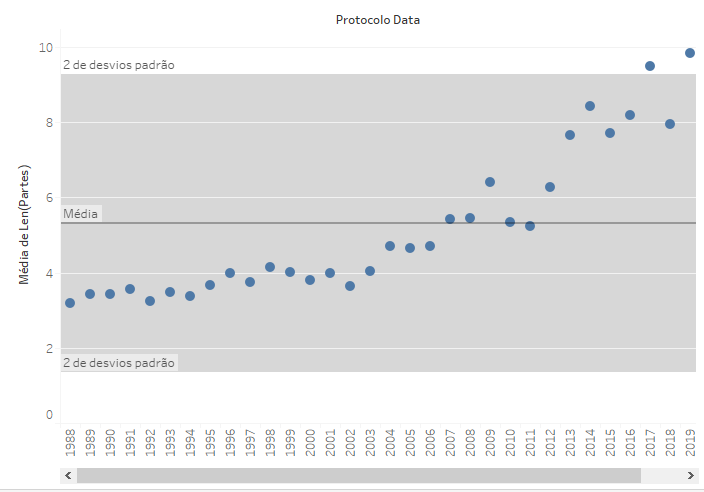
Assim, compreende-se que a média é uma reta em torno da qual os valores se distribuem, mas muitas vezes ela decorre de valores muito extremos, alguns para cima e outros para baixo, o que faz com que a faixa necessária para abarcar a maior parte deles seja bastante ampla (ou seja, tenha um alto desvio padrão).
No caso desta distribuição de dados específica, a inexistência de valores aberrantes (outliers) provavelmente decorre do fato de que fizemos uma agregação anual de dados, o que faz com que 6000 processos sejam reduzidos a poucas dezenas de entradas. Quanto menor a agregação, nesse caso, maior será a dispersão. Veja o que ocorre quando mudamos o gráfico acima, transformando-o em um gráfico trimestral, anual, mensal e diário.
Como estamos medindo a média de partes, e todo processo tem partes, não existe uma dispersão para baixo, mas apenas para cima. É de se esperar que cada processo tenha ao menos um requerente, um advogado e um interessado, o que faz com que valores abaixo de 3 causem inclusive estranhamento.
No gráfico com agregação trimestral, vemos que alguns valores começam a se distanciar mais do limite superior dos 2 desvios padrão, mas note que somente 3 valores são 2x maiores que a média e eles somam apenas 1,5% dos casos. Você pode explorar esses selecionando os pontos que quer analisar e observando o resumo, como mostra o video abaixo.
O número de elementos que fica acima (ou abaixo) de dois desvios padrão soma menos de 5% dos casos, por mais que a sua grande dispersão faça com que o gráfico diário pareça que exista uma proporção maior de casos extremos, dado que eles são mais visíveis que o bloco de casos normais, agregados dentro da faixa de distribuição de dois desvios padrão.
De fato, existe no gráfico diário um número maior de casos extremos, mas não existe uma proporção maior de elementos fora da faixa. Diferentemente do que ocorre no gráfico com agregação anual, podemos observar situações verdadeiramente aberrantes, com dias que têm um número médio de partes mais de dez vezes superior à média geral.
Para identificar os casos aberrantes (e eventualmente excluí-los) de nossos cálculos, é mais comum usarmos alguns parâmetros que se ligam à mediana, e não a média.
3.2 Mediana e quartis
A média é um valor muito influenciado pela presença de valores extremos, e por isso mesmo ela não seve adequadamente para localizar esses elementos muito distantes padrão, que impactam diretamente no seu valor. Já a mediana nos oferece um parâmetro mais razoável frente ao qual mensurar os outliers, pois ela não é impactada por esses valores aberrantes.
Isso ocorre porque a mediana não envolve uma soma de todos os valores, mas é centrado na contagem do número de objetos. Voltemos ao nosso gráfico mais simples, de número de partes por ano, e comparemos os valores da média e da mediana. No video abaixo, você pode ver como inserir a mediana e, também, alterando o rótulo, inserir no gráfico tanto o nome do cálculo (Mediana) quanto o valor.
Repare que a média é 5.3, enquanto a mediana é 4.8. Esses valores são próximos, o que sugere que a influência de outliers não distorce de forma intensa o valor da média. Mas como identificar os outliers?
O modo padrão está em dividir o gráfico em duas partes com igual contagem, por meio da mediana, e dividir novamente cada uma dessa partes novamente na metade. Isso nos oferece o que chamamos de Quartis: uma divisão do número de elementos plotados em 4 partes iguais, e a identificação dos valores dos elementos que marcam essas transições.
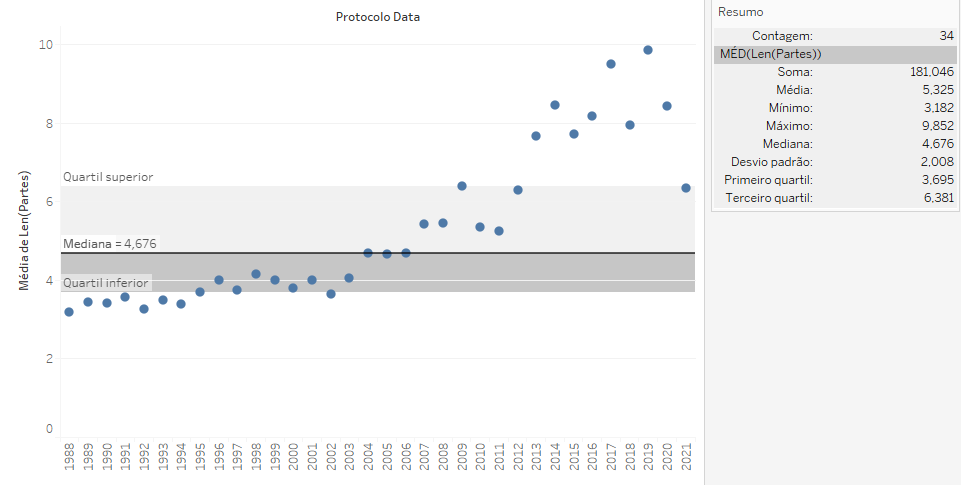
No caso do nosso gráfico, percebe-se que:
- 1/4 dos elementos está localizado na faixa entre o mínimo (3.182) e o primeiro quartil (quartil inferior = 3.695),
- 1/4 dos elementos está distribuído entre o primeiro e o segundo quartil (a mediana = 4.676)
- 1/4 dos elementos está distribuído entre a mediana e o terceiro quartil (quartil superior = 6.381)
- 1/4 dos elementos está localizado acima do quartil superior.
Portanto, metade dos elementos está distribuído entre o primeiro e o terceiro quartis. Assim, a faixa entre o quartil inferior e o quartil superior corresponde ao intervalo de valores nos quais se distribui metade dos elementos contidos no conjunto analisado. A amplitude dessa faixa é o que chamamos de diferença entre quartis (Inter Quartile Range = IQR), e esse é o parâmetro que utilizamos para avaliar a existência de valores aberrantes.
Por convenção, consideramos outlier um valor que fica mais de 1,5 IQR acima ou abaixo do valor da mediana. Note que a mediana não fica no centro do IQR, visto que a distância entre a mediana e os quartis é influenciada pelo grau de dispersão dos valores. Você pode fazer esses cálculos, mas também pode simplesmente utilizar um gráfico de caixa, que plota exatamente esse resultado.
O resutaldo é um gráfico que é pouco usual para os juristas, mas que indica justamente o que estávamos procurando:
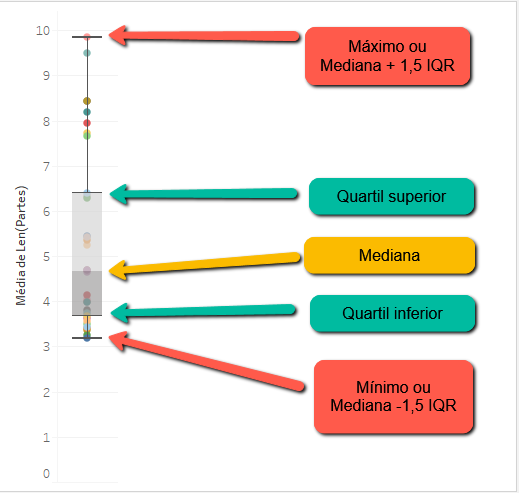
Esse gráfico mostra que os valores acima do quartil superior são mais dispersos que os que ficam abaixo do 1Q, mas não existem valores aberrantes, pois todos eles estão dentro das linhas superiores e inferiores. Todavia, se usamos agregações menores, começam a aparecer valores aberrantes, como no gráfico de média semanal de partes, em que 7,1% das semanas está mais de 1,5 IQR acima da mediana. São cerca de 7% das semanas, que somam quase 21% do número de partes, ou seja, ficam aproximadamente 3x acima da média.

Experimente selecionar e excluir esses valores aberrantes e voltar o gráfico para a agregação anual, e você verá que a mediana praticamente se igualará à média, pois elas corresponderiam a 4,7 e 4,5. Inobstante, a exclusão de 7% dos casos pode introduzir distorções relevantes no quadro geral, sendo que a a exclusão de 1% dos casos (16 semanas) mais extremos teria um impacto geral pequeno, como mostra o video abaixo.
Nesse caso, a exclusão de outliers pode ser relevante para a análise centrada em uma agregação por dias ou semanas, mas não se mostra relevante em agregações maiores, como meses e anos, que são pouco impactados pela existência de dias outliers.
Apesar disso, você aprendeu a identificar outliers e a excluí-los dos seus cálculos, se for necessário. E isso pode ser feito apenas por meio de operações nos gráficos, sem a necessidade de fazer cálculos elaborados.
3.3 Gráficos que utilizam contagem de ocorrências de dimensões
Dissemos antes que todo gráfico envolve alguma forma de campo numérico, pois os gráficos são úteis para perceber variações em campos que contém medidas. Porém, há uma forma pela qual podemos observar dimensões e gerar gráficos a partir delas: contando quantas vezes certas dimensões estão presentes em certos conjuntos.
Esse tipo de estratégia permite a criação de um tipo de gráfico que utilizamos de forma reiterada: observação da quantidade de certos valores, em determinados períodos de tempo. Por exemplo, vocês podem criar um gráfico que insira:
- nas colunas, a data de protocolo (agregada por anos);
- nas linhas, a contagem dos processos ajuizados.
Se você simplesmente colocar esses campos nos locais adequados, o resultado será uma tabela pouco útil, como o seguinte:
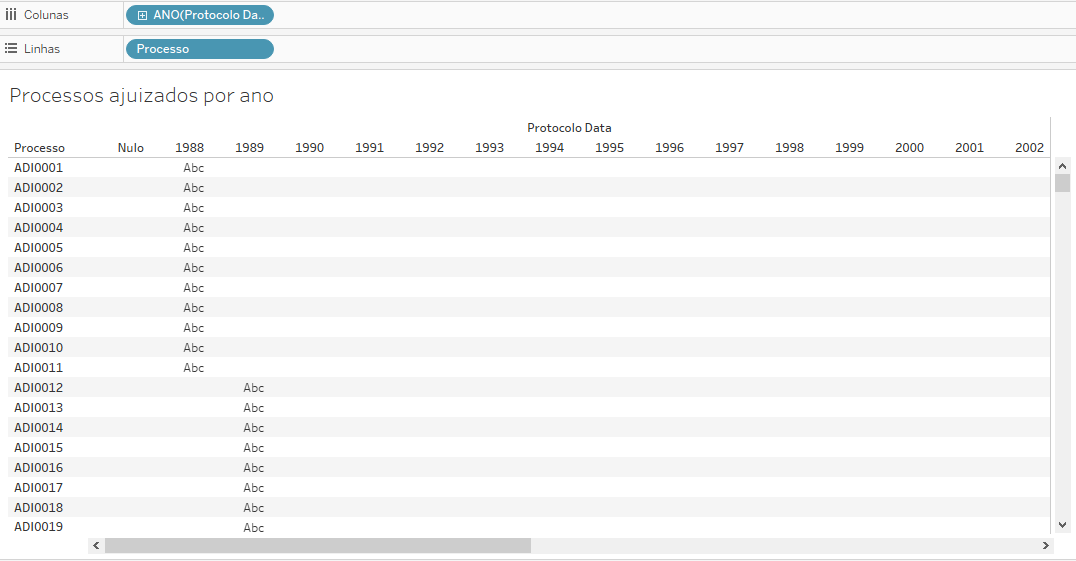
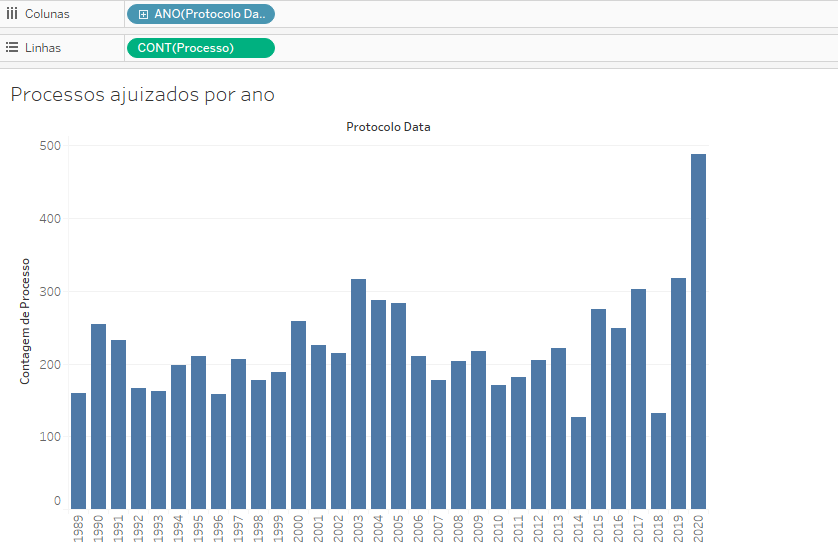
Isso acontece porque essa tabela se limita a indicar que certos processos têm data de protocolo no período indicado (por exemplo, que as ADIs de 1 a 11 foram protocoladas em 1988,). Para gerar um gráfico mais útil, podemos alterar o campo Processo, inserindo aqui uma medida derivada da string contida na variável processo: uma contagem do número de ocorrências dessa string, dentro da coluna Protocolo Data. Isso resulta em um gráfico de Processos protocolados por ano:
Você verá que convertemos a dimensão Processo em uma medida: a contagem das ocorrências de Processos. Essa alteração fez com que o gráfico de linhas fosse menos apto a revelar os padrões que estamos observando, que se toram mais claros com o gráfico de barras, que é a forma mais eficiente para exibir informações dessa natureza. Vejam que, além disso, excluímos os valores nulos (que depois podem ser revistos na base de dados, para verificar os motivos para a existência de tais elementos que não são datas válidas) e os anos de 1988 e de 2021, que não oferecem dados capazes de gerar uma comparação anualizada adequada.
Para facilitar a visualização dos dados, é importante inserir dentro das colunas alguns Rótulos, ou seja, textos que indiquem o valor de cada coluna. Esse valor pode ser observado a partir dos números contidos no eixo, mas pode ser útil inserir números dentro das barras, especialmente quando trabalhamos os gráficos em um formato maior (nas telas cheias e não em formatos pequenos, voltados a gerar imagens a serem postadas em páginas como esta).
Para inserir o rótulo, basta arrastar o campo cujo texto se deseja inserir e colocá-lo na caixa Rótulo. Lembre-se de pressionar o Ctrl enquanto faz essa operação, para que você copie o Campo CONT(Processo) para a janela de rótulos, em vez de movê-lo (porque mover retiraria esse campo da linha e alteraria o gráfico). O video abaixo mostra como fazer isso e também como escolher o alinhamento do texto (acima da barra, dentro da barra ou na base da barra).
Notem que podemos arrastar o gráfico para aumentá-lo (desde que haja espaço na janela) e que o Tableau modifica os formatos sugeridos a partir dessas alterações, mas que você pode alterar diretamente os alinhamentos, para escolher a forma exata de formatação.
3.4 Gráficos que incorporam marcações de cores
Uma das grandes vantagens dos gráficos de barras é a possibilidade de introduzir neles uma nova dimensão de complexidade, por meio de uma definição de significados para as cores.
Você pode, por exemplo, partir do gráfico anterior e introduzir um significado para as cores, arrastando o campo que você deseja representar para o quadrado Marcas:Cor. Experimente, como no video abaixo, inserir o campo Procedência na marcação de cor:
O video também mostra que, uma vez que você insere as cores, pode classificar os dados de acordo com essa distribuição das cores, utilizando o Classificar que aparece quando você clica com o botão direito sobre o campo Procedência, no painel de Marcas.
Se você não ficar feliz com as cores atribuídas automaticamente, você pode clicar sobre o botão Cor e escolher Editar Cores. Nesse caso, você pode escolher uma nova paleta de cores (não se esqueça de clicar sobre o Atribuir Paleta) ou pode atribuir individualmente as cores que desejar, aos elementos da tabela. Uma vez feita essa definição, o Tableau utilizará a mesma paleta nos gráficos posteriormente construídos com base nos mesmos campos.
Uma dos pontos fortes do Tableau é justamente possibilitar que você faça, com facilidade, gráficos de barras que segmentem os dados por meio de cores diferentes. Esse é um tipo de gráfico que tem alto poder de nos mostrar padrões interessantes nos dados e de mostrá-los aos leitores de modo claro.
Nesse caso de segmentação por cores, é melhor trabalhar com classificações com poucos elementos (de 2 a 6, por exemplo), visto que a existência de mais de uma dezena de classificações faz com que ocorram muitas barras pequenas demais para conterem os rótulos de números. Assim, quando há um número demasiado de valores, você pode agrupar os dados em classes, por meio do comando de Criar Grupo.
Uma possibilidade é criar um grupo por regiões (em vez de estados), ou dividir os estados por outros critérios (como população ou renda, por exemplo). Uma das partes mais criativas do seu trabalho é identificar o tipo de classificação que pode evidenciar padrões nos dados.
O fato de que essas classificações podem ser feitas dentro do Tableau, e não diretamente na base de dados, permite que você realize a maior parte das análises dentro desse programa e retorne ao Excel ou ao Python apenas quando for preciso aprimorar a base de dados, seja:
- corrigindo erros (como o fato de que há certas unidades que estão chamadas de UF),
- aprimorando as classificações (como a necessária diferenciação do que são os casos que impugnam leis do DF e os casos que impugnam leis federais e, somente por isso, são classificados pelo STF como tendo procedência no DF),
- criando novos campos, como um campo de tempo de tramitação ou
- aperfeiçoando o sistema de geração de cvs no seu programa.
O mais provável é que, nas primeiras análises que você fizer utilizando o Tableau, você descubra algumas limitações e imperfeições nos seus dados, que exigirão que você faça ajustes na base de dados até que ela se torne suficientemente robusta para sustentar as suas conclusões.
Lembre-se que uma base de dados perfeita não é factível. Toda base terá alguns problemas, e a sua função é ajustá-la enquanto o custo-benefício vale a pena. Existem muitos erros em uma base que vale a pena corrigir, pois eles têm grande impacto nos resultados (como a mencionada distinção entre processo do DF e processo Federal, por exemplo).
Porém, chega-se a um ponto em que o trabalho para corrigir os equívocos não resulta em análises substancialmente diversas, e você pode vir a gastar dias de trabalho para aprimorar uma base que já é suficientemente boa. É difícil encontrar esse ponto de equilíbrio, mas é preciso ter em mente que este é um daqueles casos em que o bom (no sentido de suficiente) é inimigo do ótimo, pois o esforço para chegar a uma base perfeita consumirá um trabalho desmesurado e provavelmente não terá impacto efetivo nas suas análise.